
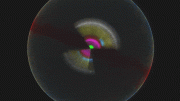
An artist’s impression of what the Milky Way might look like seen from above. The colored rings show the rough extent of the fossil galaxy known as Heracles. The yellow dot shows the position of the Sun. Credit: Danny Horta-Darrington (Liverpool John Moores University), NASA/JPL-Caltech, and the SDSS
Scientists working with data from the Sloan Digital Sky Surveys’ Apache Point Observatory Galactic Evolution Experiment (APOGEE) have discovered a “fossil galaxy” hidden in the depths of our own Milky Way.
This result, published today (November 20, 2020) in Monthly Notices of the Royal Astronomical Society, may shake up our understanding of how the Milky Way grew into the galaxy we see today.
“APOGEE lets us pierce through that dust and see deeper into the heart of the Milky Way than ever before.” — Ricardo Schiavon
The proposed fossil galaxy may have collided with the Milky Way ten billion years ago, when our galaxy was still in its infancy. Astronomers named it Heracles, after the ancient Greek hero who received the gift of immortality when the Milky Way was created.
The remnants of Heracles account for about one third of the Milky Way’s spherical halo. But if stars and gas from Heracles make up such a large percentage of the galactic halo, why didn’t we see it before? The answer lies in its location deep inside the Milky Way.
“To find a fossil galaxy like this one, we had to look at the detailed chemical makeup and motions of tens of thousands of stars,” says Ricardo Schiavon from Liverpool John Moores University (LJMU) in the UK, a key member of the research team. “That is especially hard to do for stars in the center of the Milky Way, because they are hidden from view by clouds of interstellar dust. APOGEE lets us pierce through that dust and see deeper into the heart of the Milky Way than ever before.”

An all-sky image of the stars in the Milky Way as seen from Earth. The colored rings show the approximate extent of the stars that came from the fossil galaxy known as Heracles. The small objects to the lower right of the image are the Large and Small Magellanic Clouds, two small satellite galaxies of the Milky Way. Credit: Danny Horta-Darrington (Liverpool John Moores University), ESA/Gaia, and the SDSS
APOGEE does this by taking spectra of stars in near-infrared light, instead of visible light, which gets obscured by dust. Over its ten-year observational life, APOGEE has measured spectra for more than half a million stars all across the Milky Way, including its previously dust-obscured core.
Graduate student Danny Horta from LJMU, the lead author of the paper announcing the result, explains, “Examining such a large number of stars is necessary to find unusual stars in the densely-populated heart of the Milky Way, which is like finding needles in a haystack.”
To separate stars belonging to Heracles from those of the original Milky Way, the team made use of both chemical compositions and velocities of stars measured by the APOGEE instrument.
“Of the tens of thousands of stars we looked at, a few hundred had strikingly different chemical compositions and velocities,” Horta said. “These stars are so different that they could only have come from another galaxy. By studying them in detail, we could trace out the precise location and history of this fossil galaxy.”
This movie shows a computer simulation of a galaxy like the Milky Way. The movie fast-forwards through simulated time from 13 billion years ago to today. The main galaxy grows as many small galaxies merge with it. Heracles resembles one of the smaller galaxies that merged with the Milky Way early in the process. Credit: Video built by Ted Mackereth based on the EAGLE simulations
Because galaxies are built through mergers of smaller galaxies across time, the remnants of older galaxies are often spotted in the outer halo of the Milky Way, a huge but very sparse cloud of stars enveloping the main galaxy. But since our Galaxy built up from the inside out, finding the earliest mergers requires looking at the most central parts of the Milky Way’s halo, which are buried deep within the disc and bulge.
Stars originally belonging to Heracles account for roughly one third of the mass of the entire Milky Way halo today – meaning that this newly-discovered ancient collision must have been a major event in the history of our Galaxy. That suggests that our Galaxy may be unusual, since most similar massive spiral galaxies had much calmer early lives.
“As our cosmic home, the Milky Way is already special to us, but this ancient galaxy buried within makes it even more special,” Schiavon says.
Karen Masters, the Spokesperson for SDSS-IV comments, “APOGEE is one of the flagship surveys of the fourth phase of SDSS, and this result is an example of the amazing science that anyone can do, now that we have almost completed our ten-year mission.”
And this new age of discovery will not end with the completion of APOGEE observations. The fifth phase of the SDSS has already begun taking data, and its “Milky Way Mapper” will build on the success of APOGEE to measure spectra for ten times as many stars in all parts of the Milky Way, using near-infrared light, visible light, and sometimes both.
Reference: “Evidence from APOGEE for the presence of a major building block of the halo buried in the inner Galaxy” by Danny Horta, Ricardo P Schiavon, J Ted Mackereth, Joel Pfeffer, Andrew C Mason, Shobhit Kisku, Francesca Fragkoudi, Carlos Allende Prieto, Katia Cunha, Sten Hasselquist, Jon Holtzman, Steven R Majewski, David Nataf, Robert W O’Connell, Mathias Schultheis and Verne V Smith, 20 November 2020, Monthly Notices of the Royal Astronomical Society.
DOI: 10.1093/mnras/staa2987








Hi I taught the way to measure movement using light speeds. What did it add up to I know it has started better measurements and how is fiberoptic as circuitry
What does that have anything to do with this?
It would have been useful, if somewhere in the article there was an explanation of what a ‘fossil galaxy’ is?
So, here we have a very, very, ancient group of stars which had each ignited and matured individually at some point in the past.
After presumably at least four Billion years, one of those stars collapsed into a Black Hole and pulled the others in the region toward it, forming, likely after a Billion or more years, a new small galaxy.
That galaxy wandered the cosmic expanse for a while- let’s say at least another two Billion years- until it collided with a younger galaxy (whose own stars took many Billions of years to form and coalesce- clearly long enough an age difference to clearly distinguish them chemically from the older stars). This new family of stars then existed for a few Billion years until their collective assemblage collided and coalesced with other younger galaxies- forming, after many Billions of years more, what we now know in modern times as ‘The Milky Way’.
The evidence of this process is detailed beautifully in the animation, which clearly demonstrates the complex history of collisions that would have to have taken place to reach the current structure we have today. The animation runs for seconds, but the process it portrays ran for eons.
Yet we are expected to believe that our universe is only 13.7 Billion years old.
*coughs*
So, here we have a very, very, ancient group of stars (fossil stars) each of which ignited and matured individually at some point in the past.
After presumably at least four Billion years, one of those stars collapsed into a Black Hole and pulled the others in the region toward it, forming, likely after a Billion or more years, a new small galaxy.
That galaxy wandered the cosmic expanse for a while- let’s say at least another two Billion years (I’d imagine more like ten)- until it collided with a younger galaxy (whose own stars took a few Billions of years to form and coalesce). This new family of stars then existed for a few Billion years until their collective assemblage collided and coalesced with other younger galaxies- forming, after many Billions of years more, what we now know in modern times as ‘The Milky Way’.
The evidence of this process is detailed beautifully in the animation, which clearly demonstrates the complex history of collisions that would have to have taken place to reach the current structure we have today. The animation runs for seconds, but the process it portrays ran for eons.
Yet we are expected to believe that our universe is only 13.7 Billion years old.
*coughs*
See also Kraken dwarf galaxy et al: https://scitechdaily.com/kraken-reveals-itself-astrophysicists-reconstruct-the-galaxy-merger-history-of-our-home-galaxy/#comment-569648