Even if a black hole can be described with a mathematical model, it doesn’t mean it exists in reality. Some theoretical models are unstable: though they can be used to run mathematical calculations, from the point of view of physics they make no sense. A physicist from RUDN University developed an approach to finding such instability regions. Credit: RUDN University
Physicist Develops Software Solution to Measure Black Hole Stability
Even if a black hole can be described with a mathematical model, it doesn’t mean it exists in reality. Some theoretical models are unstable: though they can be used to run mathematical calculations, from the point of view of physics they make no sense. A physicist from RUDN University developed an approach to finding such instability regions. The work was published in the Physics of the Dark Universe journal.
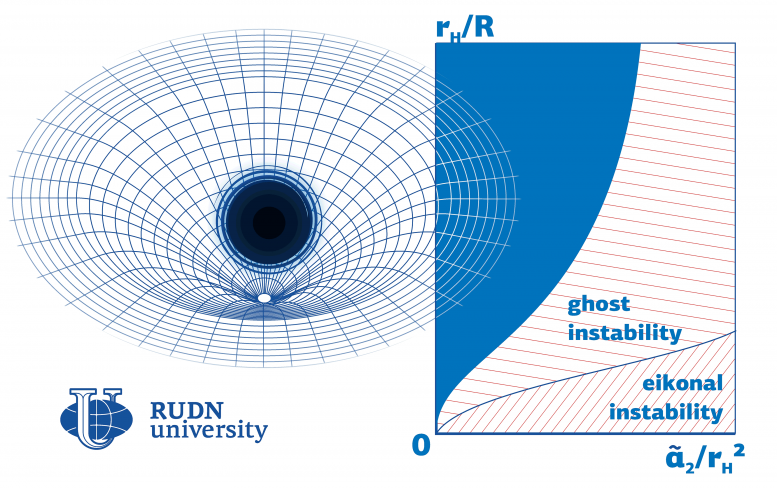
The existence of black holes was first predicted by Einstein’s general theory of relativity. These objects have so strong gravitational pull that nothing, not even light, can escape them. Dense and massive, black holes deform space-time (a physical construct with three spatial and one temporal dimension). Many mathematical models used to describe black holes include corrections to account for such space-time curvatures. The main condition of existence for every black hole model is its stability in cases of minor spatial or temporal changes. Mathematically unstable black holes make no physical sense, as the objects they describe cannot exist in reality. A physicist from RUDN University suggested a method to identify black hole instability parameters in 4D space-time.
“For a model to be considered feasible, a black hole described by it has to remain stable in case of minor space-time fluctuations. One of the most promising approaches to developing alternative gravity theories includes adding corrections to Einstein’s equation, including the fourth-order Gauss-Bonnet correction and the Lovelock correction that provides a higher level of generalization,” said Roman Konoplya, a researcher at the Educational and Research Institute of Gravitation and Cosmology, RUDN University.
The physicist studied stability in the Einstein-Gauss-Bonnet theory in which a black hole is described by Einstein’s equation with a fourth additional component. Previously, he had focused on a different mathematical description of a black hole, the so-called Lovelock theory, that describes a black hole as a sum of an infinite number of components. The instability region turned out to be closely associated with the values of the so-called coupling constants: numerical coefficients by which the corrections to Einstein’s equation are multiplied.
According to the physicist, the Einstein-Gauss-Bonnet model does not provide for the existence of small black holes, because if coupling constants are relatively big compared to other parameters (such as the radius of a black hole), the model almost always turns out to be unstable. The stability region is much bigger if the coupling constant has a negative value. Based on these calculations, he and his team developed a program to calculate black hole stability based on any of its parameters.
“Our approach helps test black hole models for stability. We made the code publicly available so that any of our colleagues could use it to calculate instability regions for models with an unspecified set of parameters,” added Roman Konoplya.
Reference: “(In)stability of black holes in the Einstein–Gauss–Bonnet and Einstein–Lovelock gravities” by R. A. Konoplya and A. Zhidenko, 7 August 2020, Physics of the Dark Universe.
DOI: 10.1016/j.dark.2020.100697








Hmm.. interesting!
The singularities of ordinary General Relativity can be avoided by considering the (mathematically well defined) Einstein-Yang-Mills-Dirac-Higgs System which is (heuristically) the super-classical limit of the (not mathematically well-defined) Standard Model. This system has complete solutions without singularities, solitons, and a Cyclic Universe solution. (The system has negative energy density; hence doesn’t satisfy the positivity conditions in the Penrose-Hawking Singularity Theorems.) The E-Y-M-D-H equations provide an alternative approach to a Cyclic Universe which Penrose has recently been advocating. They also imply that the massive compact objects now classified as Black Holes are actually Quark Stars, possibly with event horizons, but without singularities. A Super version of the above-including super-neutrinos-might be needed to explain Dark Matter. The E-Y-M-D-H is also a totally geometricized theory as a non-commutative geometry; the charge e and the mass m of the electron are geometric invariants of the non-commutative geometry analogous to pi. Unfortunately, there are quantum phenomena, such as EPR, for which this beautiful theory doesn’t make adequate predictions.
David A. Edwards
http://alpha.math.uga.edu/~davide/
Wow, what if there are no black holes, but they are actually just some Cosmic Drain Pipe, giant Langoliers :-), that suck all used space-time in, and ejects it out “on the other side” for recycling.
… if determinism gets into a black whole, what you get as a result? …
… physicists crying, …
“Even if a Black Hole Can Be Described With a Mathematical Model, It Doesn’t Mean It Exists in Reality ”
Wow, this is the most shocking confession I’ve ever seen headlined in astrophysics. Might be a bell weather moment in fact. And of course, by extension, it applies to every other scientific assertion/theory based on mathematical models, doesn’t it?
Isn’t this a moot point already? Have they not provided evidence of a black hole recently now, taking it from theory to fact? Im sure im right if I’m wrong then hands down, I apologise.