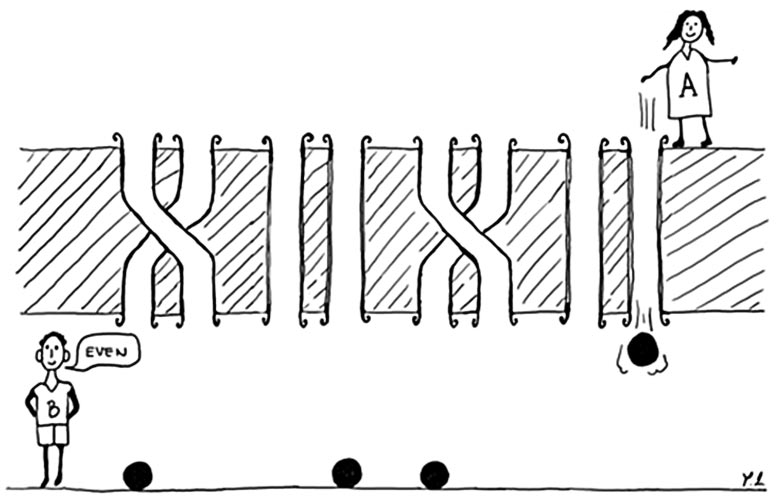
The figure pictures the simplest example of parity games. Alice (A) flicks a certain number of marbles towards Bob (B), with the aim of learning whether the number of twisted tubes is even or odd. The players need four ordinary classical marbles to complete the task. In contrast, already two quantum marbles would suffice. Credit: © Borivoje Dakić
As Richard Feynman famously put it, “the double slit experiment is absolutely impossible to explain in any classical way and has in it the heart of quantum mechanics. In reality, it contains the only mystery.”
Indeed, in this experiment, a quantum particle behaves as if it was at two distinct locations at the same time, and exhibits paradigmatic wave-like phenomena such as interference. However, it was later noted that multi-slit experiments show that the degree of delocalization of quantum particles has its limits, and that in a certain sense, quantum particles cannot be simultaneously delocalized at more than two locations.
This limitation has created a puzzle that to this day has not yet been completely resolved. Researchers at the University of Vienna and IQOQI-Vienna (Austrian Academy of Sciences) have made a significant step towards understanding this problem by reformulating interference experiments in terms of information-theoretic games. Their analysis, which has recently appeared in the journal Quantum, provides an intuitive way of thinking about interference phenomena and its limitations, thereby paving the way towards solving the aforementioned puzzle.
One of the most striking features of quantum mechanics is the superposition principle. This principle can be most easily illustrated via the double-slit experiment, which involves a particle that is sent through a plate pierced with two slits. According to our common everyday intuitions, one might expect the particle to always pass either through one slit, or through the other.
However, quantum mechanics implies that the particle can in a certain sense pass through both slits at the same time, that is, it can be in a superposition of two locations at the same time. This possibility underlies the phenomenon of quantum interference, i.e. the striking wave-like behavior exhibited by quantum particles. Now, is there a way to quantify the degree to which quantum particles can be de-localized? Does quantum theory allow particles to traverse more than two paths at the same time? In order to understand these questions, physicists have analyzed “multi-slit experiments” (Sorkin, Rafael D. “Quantum mechanics as quantum measure theory.”
Modern Physics Letters A 9.33 (1994): 3119-3127.), which differ from the double-slit experiment only in the number of slits: for example, a triple-slit experiment involves a particle sent through three slits. One may think that if a quantum particle can pass through two slits at the same time, it should also be able to simultaneously pass through three, four, or any number of slits. Surprisingly, it was immediately noted that any pattern obtained in multi-slit experiments can be explained by the particle always passing through at most two slits at the same time. Even though this feature is mathematically fully understood, the following questions remain unanswered: is there a physical reason for the apparent asymmetry between the double-slit experiment and multi-slit experiments? What underlies this somewhat arbitrary limitation on the “delocalization” of quantum particles?
In their recent work, Sebastian Horvat and Borivoje Dakić, researchers at the University of Vienna and IQOQI-Vienna (Austrian Academy of Sciences), have made a significant step towards understanding this problem by tackling it with information theory. Namely, they have reformulated interference phenomena and multi-slit experiments in terms of “parity games,” the simplest instance of which is illustrated in the figure.
The game involves two players, Alice and Bob, who are separated by a wall pierced with four pairs of tubes. Each pair of tubes can either be straight or twisted, and the number of twisted pairs is unknown both to Alice and to Bob. Furthermore, Alice has at disposal a certain number of marbles that she can flick through the tubes towards Bob; the players can use these marbles to learn something about the structure of the tubes. The goal of the game is for the players to cooperate and to find out whether the total number of twisted pairs is even or odd, by using the least possible number of marbles.
Now, suppose that Alice throws one marble through one of the tubes, for example through the second one. Bob can then easily infer whether the first pair of tubes is straight or twisted by simply checking whether the marble has fallen through the second tube or through the first one. Analogously, if Alice has at disposal four marbles, she can flick each of them through the right tube of each pair (as it is the case in the figure). Bob can then straightforwardly infer the number of twisted pairs, and thus whether this number is even or odd, thereby winning the game. However, if the number of tubes’ pairs exceeds the number of marbles that Alice has at disposal, then the game cannot be won, as there will always be at least one tubes’ pair, about which Bob can gather no information whatsoever. Therefore, in order to win the game, the players need to use as many marbles as there are pairs of tubes.
On the other hand, quantum mechanics, and more specifically, the superposition principle, enables the players to win the game illustrated in the figure by using only two “quantum marbles!” One way of understanding where this enhancement is coming from is to remember, as it was stated earlier, that a quantum particle can “pass through two locations at the same time.” Two quantum marbles can thus “simultaneously pass through four locations,” thereby mimicking the behavior of four ordinary (classical) marbles. “In this game, marbles behave analogously to tokens that can be inserted through the tubes.
When Alice inserts an ordinary classical marble, it is as if she inserted 1 penny. On the other hand, as quantum theory allows marbles to “pass through 2 tubes at the same time,” each quantum marble is worth 2 pennies. The value of the tokens is additive: for example, in order to win the game, Alice can either insert 4 classical marbles or 2 quantum marbles, as the total token value is in both cases equal to 4 pennies,” explains Sebastian Horvat.
On the other hand, recall that a quantum particle cannot pass through more than two locations at the same time: this is reflected in the fact that Alice and Bob cannot win the game by using less than two quantum marbles. Hence, in order to win the game, the number of quantum marbles sent by Alice needs to be equal to at least half of the total number of tubes’ pairs.
In their work, the researchers have analyzed more general formulations of this game and have studied the players’ performance depending on the number of particles and on whether the particles are classical, quantum, or of more general and hypothetical kinds. Borivoje Dakić adds: “These hypothetical particles possess higher information-processing power, that is, their corresponding tokens are valid more than 2 pennies. It is not a priori clear why Nature should prefer classical and quantum particles over these hypothetical ones: this is something that we still have to study in the future.”
All in all, parity games provide an alternative description of quantum interference within a more general and intuitive framework, which will hopefully shed light on novel features of quantum superposition, similarly to how the study of quantum entanglement has been deepened through the formulation of the so-called “nonlocal games” (Brunner, Nicolas, et al. “Bell nonlocality.” Reviews of Modern Physics 86.2 (2014): 419.).
Reference: “Interference as an information-theoretic game” by Sebastian Horvat and Borivoje Dakić, 8 March 2021, Quantum.
DOI: 10.22331/q-2021-03-08-404
arXiv: 2003.12114v4







There are no “Particles.” It’s all waves all the time Bubala. End of paradox.
Are they not just describing probability here
Why should the competing observers play the game, if the outcome is clear and the most elegant methode to win the game is for the starting player to select the coin value of the marble equivalent to the number of tubes divided by the number of observers on the other side of the quadrupol-slit-experiment, where two observers interact with two spacially seperated pieces of matter in the light of a third observer, who measures the outcome of the game and decides which of the player has won, as they can not observe each other through a twisted tube by a lightwave.
Single-particle interference experiments are performed that require the simultaneous superposition (in any reference frame) of far more than two classical trajectories. Heisenberg’s uncertainty principle rules out not only a single history for any particle, but just two histories, or 137 of them, etc. Consider the smallest number of trajectories one needs to explain how a single electron contributes to an atomic orbital or molecular bond.
I love the scientific communities information and theories. I think the explanation for the different wave forms in the double slit experiment could be when the observer is present it changes the vibration or it recognizes a different vibration. So it acts different. Just a thought.
c^3et8mmmmmt
Love this article!
nice game, thx!