
Researchers discovered entangled photon quantum states indistinguishable without complex numbers and conducted an experiment affirming their importance in quantum mechanics.
An international research team has proven that the imaginary part of quantum mechanics can be observed in action in the real world.
For almost a century, physicists have been intrigued by the fundamental question: why are complex numbers so important in quantum mechanics, that is, numbers containing a component with the imaginary number i? Usually, it was assumed that they are only a mathematical trick to facilitate the description of phenomena, and only results expressed in real numbers have a physical meaning. However, a Polish-Chinese-Canadian team of researchers has proved that the imaginary part of quantum mechanics can be observed in action in the real world.
We need to significantly reconstruct our naive ideas about the ability of numbers to describe the physical world. Until now, it seemed that only real numbers were related to measurable physical quantities. However, research conducted by the team of Dr. Alexander Streltsov from the Centre for Quantum Optical Technologies (QOT) at the University of Warsaw with the participation of scientists from the University of Science and Technology of China (USTC) in Hefei and the University of Calgary, found quantum states of entangled photons that cannot be distinguished without resorting to complex numbers. Moreover, the researchers also conducted an experiment confirming the importance of complex numbers for quantum mechanics. Articles describing the theory and measurements have just appeared in the journals Physical Review Letters and Physical Review A.
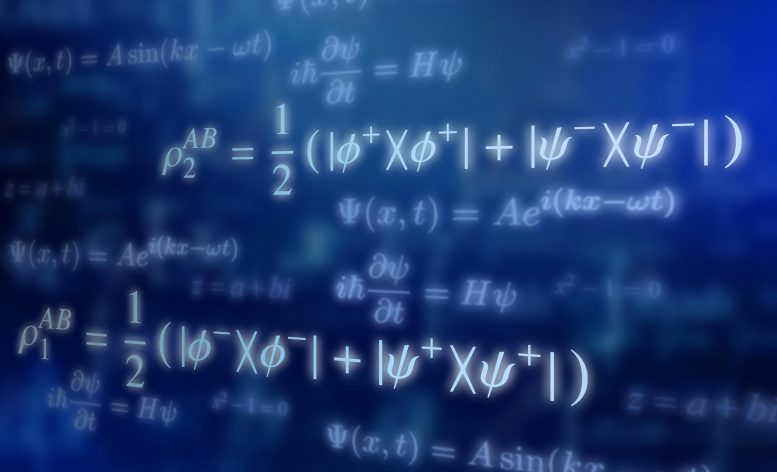
Photons can be so entangled that within quantum mechanics their states cannot be described without using complex numbers. Credit: QOT/jch
“In physics, complex numbers were considered to be purely mathematical in nature. It is true that although they play a basic role in quantum mechanics equations, they were treated simply as a tool, something to facilitate calculations for physicists. Now, we have theoretically and experimentally proved that there are quantum states that can only be distinguished when the calculations are performed with the indispensable participation of complex numbers,” explains Dr. Streltsov.
Complex numbers are made up of two components, real and imaginary. They have the form a + bi, where the numbers a and b are real. The bi component is responsible for the specific features of complex numbers. The key role here is played by the imaginary number i, i.e. the square root of -1.
There is nothing in the physical world that can be directly related to the number i. If there are 2 or 3 apples on a table, this is natural. When we take one apple away, we can speak of a physical deficiency and describe it with the negative integer -1. We can cut the apple into two or three sections, obtaining the physical equivalents of the rational numbers 1/2 or 1/3. If the table is a perfect square, its diagonal will be the (irrational) square root of 2 multiplied by the length of the side. At the same time, with the best will in the world, it is still impossible to put i apples on the table.

The photon source used to produce quantum states requiring description by complex numbers. Credit: USTC
The surprising career of complex numbers in physics is related to the fact that they can be used to describe all sorts of oscillations much more conveniently than with the use of popular trigonometric functions. Calculations are therefore carried out using complex numbers, and then at the end only the real numbers in them are taken into account.
Compared to other physical theories, quantum mechanics is special because it has to describe objects that can behave like particles under some conditions, and like waves in others. The basic equation of this theory, taken as a postulate, is the Schrödinger equation. It describes changes in time of a certain function, called the wave function, which is related to the probability distribution of finding a system in a specific state. However, the imaginary number i openly appears next to the wave function in the Schrödinger equation.
“For decades, there has been a debate as to whether one can create coherent and complete quantum mechanics with real numbers alone. So, we decided to find quantum states that could be distinguished from each other only by using complex numbers. The decisive moment was the experiment where we created these states and physically checked whether they were distinguishable or not,” says Dr. Streltsov, whose research was funded by the Foundation for Polish Science.
The experiment verifying the role of complex numbers in quantum mechanics can be presented in the form of a game played by Alice and Bob with the participation of a master conducting the game. Using a device with lasers and crystals, the game master binds two photons into one of two quantum states, absolutely requiring the use of complex numbers to distinguish between them. Then, one photon is sent to Alice and the other to Bob. Each of them measures their photon and then communicates with the other to establish any existing correlations.
“Let’s assume Alice and Bob’s measurement results can only take on the values of 0 or 1. Alice sees a nonsensical sequence of 0s and 1s, as does Bob. However, if they communicate, they can establish links between the relevant measurements. If the game master sends them a correlated state, when one sees a result of 0, so will the other. If they receive an anti-correlated state, when Alice measures 0, Bob will have 1. By mutual agreement, Alice and Bob could distinguish our states, but only if their quantum nature was fundamentally complex,” says Dr. Streltsov.
An approach known as quantum resource theory was used for the theoretical description. The experiment itself with local discrimination between entangled two-photon states was carried out in the laboratory at Hefei using linear optics techniques. The quantum states prepared by the researchers turned out to be distinguishable, which proves that complex numbers are an integral, indelible part of quantum mechanics.
The achievement of the Polish-Chinese-Canadian team of researchers is of fundamental importance, but it is so profound that it may translate into new quantum technologies. In particular, research into the role of complex numbers in quantum mechanics can help to better understand the sources of the efficiency of quantum computers, qualitatively new computing machines capable of solving some problems at speeds unattainable by classical computers.
References:
“Operational Resource Theory of Imaginarity” by Kang-Da Wu, Tulja Varun Kondra, Swapan Rana, Carlo Maria Scandolo, Guo-Yong Xiang, Chuan-Feng Li, Guang-Can Guo and Alexander Streltsov, 1 March 2021, Physical Review Letters.
DOI: 10.1103/PhysRevLett.126.090401
“Resource theory of imaginarity: Quantification and state conversion” by Kang-Da Wu, Tulja Varun Kondra, Swapan Rana, Carlo Maria Scandolo, Guo-Yong Xiang, Chuan-Feng Li, Guang-Can Guo and Alexander Streltsov, 1 March 2021, Physical Review A.
DOI: 10.1103/PhysRevA.103.032401
The Centre for Quantum Optical Technologies at the University of Warsaw (UW) is a unit of the International Research Agendas program implemented by the Foundation for Polish Science from the funds of the Intelligent Development Operational Programme. The seat of the unit is the Centre of New Technologies at the University of Warsaw. The unit conducts research on the use of quantum phenomena such as quantum superposition or entanglement in optical technologies. These phenomena have potential applications in communications, where they can ensure the security of data transmission, in imaging, where they help to improve resolution, and in metrology to increase the accuracy of measurements. The Centre for Quantum Optical Technologies at the University of Warsaw is actively looking for opportunities to cooperate with external entities in order to use the research results in practice.







You can put i apples on a table as follows.
If we say an apple is represented by complex number a * bi, that is equivalent to an apple with amplitude a and frequency of b. We think of an apple as having a constant value, but if say you ate it and planted the seeds, and waited until another apple grew, you could say it has a frequency, say of five years. So with an apple of size a, and frequency b = 5 years, it makes sense to represent it by a complex number.
This is probably because i itself has a repetitive( therefore wavelike) exponential sequence: i⁰ = 1, i¹ = i, i² = -1, i³ = -i, i⁴ = 1, etc..
There is absolutely a physical meaning for i. It is a counterclockwise rotation by 90°. Start at (1,0) on the x-y plane. Rotate by 90° twice. You end up at (-1,0). Two rotations are a “multiplication” of imaginary numbers.
Imaginery numbers are related to a “measurable, physical quantity.” Ask any engineer about real and reactive power in AC circuits.
What if we “i”magnined there were 3 apples on the table sitting next to 2 real apples: 2 + 3i.
The issue most people have is they confuse mathematical terms like real and imaginary with their general or common meaning. In mathematics, real and imaginary (or complex) numbers actually exist and are used to accurately describe actual physical systems. In the mathematical sense, imaginary or complex means the square root of -1 is needed to describe a system.
All complex numbers and functions can be equivalently represented by 2×2 real number matices. So there is nothing necessarily more “real” about imaginary numbers than there has always been about vectors and tensors.
Sorry to be a party pooper, but there’s a pretty good size group of physicists out there (and not a few computer scientists and engineers as well) who’ve known for a very long time that imaginary numbers are real — and I mean that literally. The trick lies in an extension of standard 3D vector algebra to higher dimensions and even non-Euclidean spaces, known to mathematicians as Clifford algebras although its aficionados prefer to call them geometric algebras (as Clifford himself did). These algebras are over the real numbers (i.e. they contain only real scalars) but typically contain entities that square to -1 and commute with vectors, just like complex scalars would. The difference is that these geometric imaginary units can be understood as oriented spatial magnitudes, in much the same way that vectors are understood as oriented linear magnitudes. Such geometric interpretations can go a long way towards demystifying quantum mechanics (although the do not, of course, solve the measurement problem).
For just one of the many introductions to geometric algebra out there, see http://geocalc.clas.asu.edu/html/IntroPrimerGeometricAlgebra.html
While the described experiments are informative, the talk that imaginary numbers are “real-world” and it is “first time” is a usual PR talk to gain more publicity and hence grants. I’ve seen pop-sci talks about “real” imaginary numbers some 40 years ago, only in the context of electromagnetics.
Since the square 0f imaginary part i is itself has a repetitive pattern in nature ( therefore wavelike) exponential sequence: i⁰ = 1, i¹ = i, i² = -1, i³ = -i, i⁴ = 1, etc.. it predicts the past, present and future of the probable events at quantum energy states of an events or things.
Q Sheikh
Jamshedpur, India
Mobile: +913354510, gmail : [email protected]
Of course it all exists, but some of it doesn’t matter. 😉
Harry Potter science in action…(Not understanding what quantum mechanics is all about gives you the freedom to do pseudo-science.)
Conceptually I think the problem people have is the use of the word “imaginary”, which stems I think from the misunderstanding of “negative” numbers.
For example, a “deficiency” of 1 is an interpretation of what -1 means. If you have -1 dollars, it means you owe +1 dollars. If a step forward is +1 and a step backward is -1, then -1 is just +1 step in the opposite direction. Or on a number line, to the right is + and to the left is -. Since adding positive leftward numbers is the same as subtracting positive rightward numbers, we use the same symbol for subtraction and “negatives” which are really positives in an opposite metric. We could call rightward counting by 1 as ‘1R’ and leftward counting as ‘1L’ instead of + and -.
Where it goes astray is multiplication and the commutative ordering. 5 groups of 3 items = 3 groups of 5 items = 15 items, or in our new naming, 5R x 3R = 3R x 5R = 15R. By analogy, meaning by our desired definition for consistency, 5 groups of -3 items = -3 groups of 5 items = -15 items, or 5R x 3L = 3L x 5R = 15L.
In other words, multiplying by a “negative” or “leftward” number acts to mirror across the origin, which is a new property that “positive” or “rightward” numbers don’t do. They they stay on the rightward side.
And hence starting with a leftward (negative) number and multiplying it by a leftward (negative) number mirrors it to be a rightward (positive) number, (-5)x(-5)=25 (or 5Lx5L = 25R). “Negative multiplying” represents a mirror functions.
Similarly, “negative exponents” define a reciprocal function: x^(-y) = 1/(x^y), or xR^yL = 1/(xR^yR).
This new mirroring function of multiplying negatives also adds to the solutions to the square root function. sqrt(25R) = 5R or 5L (5 or -5).
But, because of this mirroring function of multiplying leftward numbers (negatives), there are no two rightward or leftward numbers that multiply by themselves to produce a leftward number. So, you can find a square root of a leftward number within rightward or leftward (positive or negative) numbers.
No problem. Just as we did with defining leftward (negative) numbers and their interpretation (opposite direction, owing, deficiency) and their math rules, we can define another new set of numbers called Perpendicular numbers, where 1P x 1P = 1L. Et voila, we have “found” the sqrt(1L) = sqrt(-1) = 1P.
The Perpendicular number systems has its own self-consistent math function rules the same as rightward and leftward numbers. It has positive Perpendicular numbers and negative Perpendicular numbers, including how to add, subtract, multiply, divide, exponents, roots, and so forth. They all work consistently in a closed math system.
We now have 3 sets of numbers: R, L, and P. You can jump between them via math functions. You can go from R to L by subtracting larger R numbers (3R – 5R = 2L), by adding bigger L numbers (3R + 5L = 2L), or by mirroring through multiplying by an R number (3R x 5L = 15L). You can go from L to R numbers by reversing these functions.
You can go from L to P via the sqrt function, 1P = sqrt(1L) aka 1i = sqrt(-1). You can only go from R to P either via intermediary L, 1P = sqrt(4R-5R)=sqrt(1L), or by multiplying by a P number, 4Rx2P = 8P (4x2i=8i).
“Imaginary” numbers are not imaginary any more than negative numbers are imaginary. You can’t have negative things, only positive things in an opposite or mirrored direction, which is how we use negatives. They create a closed and consistent algebra.
We’ve just gotten used to translating what “negative” means in context and accept that negative numbers are therefore “real”. Imaginary numbers are similarly “real” in terms of translating them into how they are applied. Going back to normal notation (1P = i), i^2 = -1; i^3 = -i; i^4 = 1; i^5 = i; and so on. Multiplying by i rotates a number line by 90 degrees. Complex numbers then represent things that have two independent degrees of freedom.
If you go further, quaternions define 4 degrees of freedom, a+bi+cj+dk, where i^2 = j^2 = k^2 = -1, and ixj=k, jxk=i, kxi=j, and reversing the order changes the sign, ergo loses commutative property. So quaternions could represent time plus 3 perpendicular spatial dimensions, for example, scaled appropriately.
Octonians do the same with 8 dimensions. And, I’m pretty sure that is it for closed algebra systems: real (positive, negative), complex (real, imaginary), quaternions, and octonians, or 1, 2, 4, 8. No other systems work.
They all have meaning and can represent something, so long as the mathematical functions properly represent the things and we can interpret what they mean. E.g., if you walk the perimeter of a rectangle 5i x 3j = 15k, it means you define the plan of the rectangle with the normal in the k-direction, perpendicular to i and j, using the “right-hand” rule. Reversing direction, 3j x 5i = -15k = 15(-k), or a rectangle with normal in the opposite direction. Hence quaternions can be used to represent both size (15) and directionality (k) of a surface. Hence they can be “real”.
Timothy Havel’s reply concerning Clifford (geometric) algebras is correct in my opinion. The actual paper I believe after reading it is more concerned with proving the authors “resource theory of imaginarity” all of this is simply pointing to directed magnitudes in higher dimensions… nothing unreal exists.
Since they arent even sure of the standard model anymore, aren’t these physicists trying to describe using complex #s”things” they are not even sure of in the first place..? Looking for funds perhaps?
Yeah, I should note that as an electrical engineer complex numbers literally describe our entire electric grid. Ever hear of 3-phase power? Each line has the same amplitude (voltage) and frequency (50/60 Hz) but they are out of phase with each other in complex number world. Reactive power and power factors are very real. This is actually quite common knowledge among electrical and mechanical engineers.
Of course Quantum mechanics is real? Our consciousness precides, nanoseconds into A future that is governed by an infinite amount of possibilities.
From moment to moment we live on an infiteciamal small string between chaos and order. It is truly a Beautiful thing to wanderer a world where imagination is endless and we
realize numbers don’t matter without words.
Now, if you number lovers admit,
“A negative times a negative doesn’t not equal a positive; I don’t care if you turn left and look backwards. It’s no different than saying, “Two wrongs don’t make a right” I’ll respect your philosophy.
The very basic of complex number itself is dealibg with zeta function tgat oscillate between real and imaginary combination of horizontal and vertical spin directions as sum reflect zero half and also between +1 and -1 rotating vectors that converge and diverge along asymmetric regularity.This is leading to a converging string theory involved.Thenumber times any infra red waves osciilate a specific superconductive graphene phase itself is a typical example in 1.1 degree conical spin that seems to give specific superconductive outputs.It hs to deal with pressure surrounding a chemical bonding is integrated and differentiated in between in enhancing a superconductive effect.This really meansan imaginary part is really feeding a real part by experimenting with superconductivity asekectron flow in between parallelplates contributing towards asymmetric grapphics.
I’m stuck on this ..
11÷10−1×11÷10=0. But…if,you multiply 0. You get 1.1 but if you add before the x0 you get what you add.
That still doesn’t explain where the .1 disappears too. It would be imaginary.
I’m not a big brain. I just had this come to me as a big flaw in the number system itself. To me, if this cannot be solved or it’s some black hole in the matrix, 0 becomes the source of everything and nothing. It’s also means nothing is actually real. And with the quantum mechanics of things, nothing is 0 and 0 is something.
I’m sure the order of operations has something to do with it but, if, you don’t multiply by 0 and multiply any other # the .1 is involved in the final answer.
I found this while I was messing around with time. 365.25/364.25-1 second. Is 0.002745367. This is missing time. Because 365.25/364.25-1×365.25/364.25=0. And that’s where the same problem happens. Where did the 0.002745367 go? It’s still there if you multiply but it disappears if you add. And it doesn’t come back either.
When you take 1001/1000 basically just grabbing the binary by the balls as it dangles from the ascii. All those 1s and 0s begin to disappear forever. It’s like the matrix mind and anyone linking their brain to it begins to loose their minds. Was their mind even real to begin with or was their entire ego state of being just a dream? Seems as though even the quantum state can be erased too. Making what is what is and not just a bunch of whack jobs with giant heads in the sky thinking they can solve reality.
I’m not sure who said…everything is a theory. Just because the same thing always happens it doesn’t mean it will always happen. At some point it can change.
Everything is changing alright. The line has been drawn…which side your on all depends on how well you understand the unknown unknown. That is you. Numbers didn’t create you. You created numbers. Before nothing there was you right here right now.
So, all the effort to construct an idea our quantum physics is a moot point. I can smash my hand and the bone fragments, blood and skin can be called something else. It still doesn’t make it into a hand. No matter what I do to piece it together, the body is what knows how to fix it. The same goes for everything. Smashing atoms together doesn’t create. It’s not necessary unless you trying to kill yourselves. It probably why it’s so much fun to dig in the sand. It’s easy to destroy. It’s hard to create.
I say all this because I am aware of what these crazy scientists working to destroy humanity are up to. While, the majority of the world is lost in a trance believing the same ideas that less them away from themselves, there are a very few of us if flesh that have to stand up for the many. With a backing of our ancestors, I like to make a fool of myself at times.
But…. The points is….maybe, this simple 11/10-1*11/10 Explains how nothing can exist if, nothing cannot exist. If, nothing cannot exist, nothing can exist.
If, you got dizzy, chills, uneasy, or numb…your welcome. If, you didn’t….you will…
dude you are just doing math wrong.
11/10-1 =.1,
11/10=1.1,
(11/10-1)-(11/10)=-1
(11/10-1)*(11/10)=.11
when you say 11/10-1*11/10 it is (11/10)-(1*11/10) which is (11/10)-(11/10) which is 1.1-1.1 which is 0. that is not the same thing as (11/10-1)*(11/10) which is 0.1*1.1 which is 0.11
Solution to PvNP resolves geometry, and puts trigonometry in the dog house. i can be expressed geometrically and still there is an even greater dilemma when you solve the initial stage of Quantum/Relative reconciliation. The moral of the story? We are already WAY past the level of technology we need to fix earth. What are they still looking for? The ability to cheat death? The ability to wage war against god directly? Time to beam back down to Earth before these “physicists” cause a massive catastrophe that ends all life on Earth.
In electromagnetic physics, “i” is used to represent phase shifts. This makes the calculations appear simpler than when a sum of sine and cosine terms are used. So “i” is just a mathematical device. It has nothing to do with whether the result is “real.”
Interesting too because in optical fiber the light propagating in the core has a skin depth penetration into the cladding is also modeled as a mathematical “imaganery” number. However, the energy in that little bit is enough to exploit it’s real effects. I used it to build and patent a fiber optic liquid level sensor. Demonstrated it to GM as a technology demonstration for a gas level sensor.
i is no more “real” than any other mathematical concept. It’s just a human construct used as a tool to facilitate calculations. All you can say is that there are quantum states that are indistinguishable in our mathematical system without using complex numbers. That’s got nothing to do with reality.
And what is the mathematical probability of that being true? Why 50-50 of course. Either it’s true or not. Could we change that statistic with a half truth gleaned utilizing imaginary values? Sure. You think science will answer ALL the questions in the Universe? We need mystery of the unknown to retain our awe. Our fascination and awe drives our imaginations.
Complex number consists of a real number added with it an ìmaginzry number.which contains +ve square root of _1 as a factor.Thus,complex number involves in many of calculations of physìcs,like in radient energy and so on.So QC can come for calculations invoĺving complex numbers in some problems related to the stars.Often calculations need to compute pròblems còntain,e to power ix.
Òften probĺemsìn star radiation can .involves with term like,e to powèŕ ix be solved by QC.These are examples of complex numbers involvement in physics are fòund out in practical.
A complex wave function psi multiplied by it’s complex conjugate psi-star IS REAL. That’s what used on quantum mechanics.p