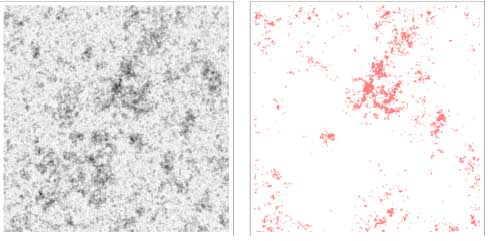
A schematic illustration of Zip’s Law for galaxies or cities. On the left is a simulated population distribution with darker spots indicating higher densities; on the right, in pink, are the locations where the population density exceeds some critical value. The distribution of pink clusters agrees with Zipf’s Law.
Abstract: The spatial distribution of people exhibits clustering across a wide range of scales, from household (∼10−2 km) to continental (∼104 km) scales. Empirical data indicates simple power-law scalings for the size distribution of cities (known as Zipf’s law) and the population density fluctuations as a function of scale. Using techniques from random field theory and statistical physics, we show that these power laws are fundamentally a consequence of the scale-free spatial clustering of human populations and the fact that humans inhabit a two-dimensional surface. In this sense, the symmetries of scale invariance in two spatial dimensions are intimately connected to urban sociology. We test our theory by empirically measuring the power spectrum of population density fluctuations and show that the logarithmic slope α=2.04±0.09, in excellent agreement with our theoretical prediction α=2. The model enables the analytic computation of many new predictions by importing the mathematical formalism of random fields.
In the last century, the linguist George Zipf noticed that the second most common word in English (“of”) was used about half as often as the most common word (“the”), the third most common word (“and”) occurred about one-third as often, and so on. This curious behavior, that the frequency of any word is inversely proportional to its ranking in the list of words, became known as Zipf’s Law. Others had noticed the same behavior for the populations of cities, namely, that the second most populous city had roughly half the population of the most populous city, the third most populous city had one-third the population, and so on. Scientists studying the detection of faint signals in a background of noise also began to notice a similar effect, with most systems having a component of noise whose intensity varied inversely with the frequency, so-called “one-over-f” noise. Theoretical statistical analyses have found many other cases in which Zipf’s Law, or close approximations to it, could result from quasi-random distributions of the element being considered, whether words or cities. There are many slight deviations, however, and no consensus exists on the origin of Zipf’s Law.
Galaxies form when the density of matter exceeds some critical value. CfA astronomers Henry Lin, a Harvard undergraduate, and Avi Loeb noted that, like galaxies, cities also might be thought of as forming once their populations exceeded some critical value, with the larger the population, the larger the city. Since Zipf’s Law applied to cities, they investigated whether it might also apply to galaxies, and why this might be the case. Rather than focusing on how the law emerges from specific situations, they argue that it occurs naturally in all statistical systems with two key properties: a two-dimensional geometry (galaxies are seen projected onto the two-dimensional plane of the sky) and a clustering behavior that is independent of size (“scale-invariance”) so that a small region looks the same as a large region. The scientists show mathematically that with these two characteristics, a Zipf-Law behavior naturally emerges. (Of course for some systems, like words, different reasons may be responsible for producing a Zipf’s Law character.) The new theory can derive Zipf’s Law and successfully predict population density fluctuations.
Reference: “Zipf’s Law from Scale-free Geometry” by Henry W. Lin and Abraham Loeb, 9 September 2015, Physical Review E.
DOI: 10.1103/PhysRevE.93.032306
arXiv:1501.00738







Be the first to comment on "Zipf’s Law from Scale-free Geometry – Like Galaxies, Like Cities"