Mathematically speaking, ocean eddies are counterparts to the black holes in space. Credit: G. Haller / ETH Zurich
According to newly published research, some of the largest ocean eddies on Earth are mathematically equivalent to the mysterious black holes of space. These eddies are so tightly shielded by circular water paths that nothing can escape from the inside of these loops, not even water.
The mild winters experienced in Northern Europe are thanks to the Gulf Stream, which makes up part of those ocean currents spanning the globe that impact on the climate. However, our climate is also influenced by huge eddies of over 150 kilometers (93 miles) in diameter that rotate and drift across the ocean. Their number is reportedly on the rise in the Southern Ocean, increasing the northward transport of warm and salty water. Intriguingly, this could moderate the negative impact of melting sea ice in a warming climate.
However, scientists have been unable to quantify this impact so far, because the exact boundaries of these swirling water bodies have remained undetectable. George Haller, Professor of Nonlinear Dynamics at ETH Zurich, and Francisco Beron-Vera, Research Professor of Oceanography at the University of Miami, have now come up with a solution to this problem. In a paper just published in the Journal of Fluid Mechanics, they developed a new mathematical technique to find water-transporting eddies with coherent boundaries.
The challenge in finding such eddies is to pinpoint coherent water islands in a turbulent ocean. The rotating and drifting fluid motion appears chaotic to the observer both inside and outside an eddy. Haller and Beron-Vera were able to restore order in this chaos by isolating coherent water islands from a sequence of satellite observations. To their surprise, such coherent eddies turned out to be mathematically equivalent to black holes.
Animation of the Agulhas Rings, ocean eddies of the black hole type.
No escape from the vortex
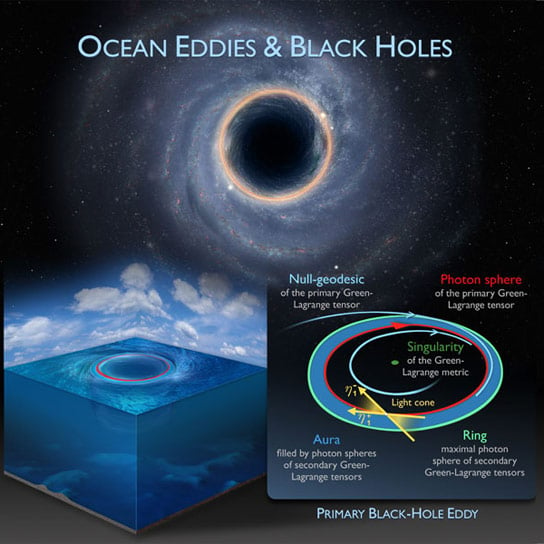
Black holes are objects in space with a mass so great that they attract everything that comes within a certain distance of them. Nothing that comes too close can escape, not even light. But at a critical distance, a light beam no longer spirals into the black hole. Rather, it dramatically bends and comes back to its original position, forming a circular orbit. A barrier surface formed by closed light orbits is called a photon sphere in Einstein’s theory of relativity.
Haller and Beron-Vera discovered similar closed barriers around select ocean eddies. In these barriers, fluid particles move around in closed loops – similar to the path of light in a photon sphere. And as in a black hole, nothing can escape from the inside of these loops, not even water.
It is precisely these barriers that help to identify coherent ocean eddies in the vast amount of observational data available. According to Haller, the very fact that such coherent water orbits exist amidst complex ocean currents is surprising.
Eddies as water taxis
Because black-hole-type ocean eddies are stable, they function in the same way as a transportation vehicle – not only for micro-organisms such as plankton or foreign bodies like plastic waste or oil, but also for water with a heat and salt content that can differ from the surrounding water. Haller and Beron-Vera have verified this observation for the Agulhas Rings, a group of ocean eddies that emerge regularly in the Southern Ocean off the southern tip of Africa and transport warm, salty water northwest. The researchers identified seven Agulhas Rings of the black-hole type, which transported the same body of water without leaking for almost a year.
Haller points out that similar coherent vortices exist in other complex flows outside of the ocean. In this sense, many whirlwinds are likely to be similar to black holes as well. Even the Great Red Spot – a stationary storm – on the planet Jupiter could just be the most spectacular example of a black-hole type vortex. ”Mathematicians have been trying to understand such peculiarly coherent vortices in turbulent flows for a very long time“, explains Haller.
Notably, the first person to describe ocean eddies as coherent water islands may well have been the American writer, Edgar Allan Poe. In his story «A Descent into the Maelstrom», he envisioned a stable belt of foam around a maelstrom. This served as inspiration for Haller and Beron-Vera, who went on to find these belts – the oceanic equivalent to photon spheres – using sophisticated mathematical formulas. Their results are expected to help in resolving a number of oceanic puzzles, ranging from climate-related questions to the spread of environmental pollution patterns.
Eddy in the Gulf of Mexico
Just after the publication of Haller’s and Beron-Vera’s results, Josefina Olascoaga, also a Professor of Oceanography in Miami, tested their new mathematical method. She unexpectedly found a large, black-hole type eddy in the Gulf of Mexico. (VIDEO) Olascoaga now uses her finding to assess the coherent transport of contamination from a possible future oil spill.
Reference: “Coherent Lagrangian vortices: the black holes of turbulence” by G. Hallera and F. J. Beron-Vera, 3 September 2013, Journal of Fluid Mechanics.
DOI: 10.1017/jfm.2013.391
arXiv:1308.2352







sounds like a bird of a feather flocks together to me,don’t water molecules attract water molecules? salt is used to melt ice,salinity concentrated, trapped in vortices continually swirling perpetuating it’s own movement,sounds like the birth of gravity in liquid form, the gaseous form in the vacuum of space is powerful enough to bend light and destroy planets? I think not,light is still intact spiralling dark energy and matter which dominates our cosmos on this side of our known dimension,light melting no,its using dark matter for locomotion of its own…how placing a series of mirrors in orbit and reflecting our suns energy at them creating our own vortex and see what happens!?
What? Keep taking the pills, Raymond Gardner sr… As for the suggestion Ocean Eddies are (Mathematically Equivalent to, ‘Black Holes’.. Well, it just goes to show what can be done through ‘Maths,
Jiggery Pokery’!
One of the most interesting facets of Black Hole is that the Polar Jets always emanate perpendicularly from the motion of the rest of the galaxy. If the Black Hole in the center of a galaxy was just an object in the center of other objects; the central black holes would regularly have their polar jets pointed in the direction of the disk of a galaxy and obviously this is not the case. That is exactly how an ocean eddy acts, just doubled on it’s self.
The draw back here is that ocean eddies are always horizontal motions with vertical polar jets. We need a far more work in a large pool of liquid with some type of dye to observe the motion of the vortexes in water or maybe even liquid hydrogen. Then the mathematicians should start looking at is the interaction of the polar jets in galaxies that are in the process of merging and then compare those interactions with vortices that have similar reactions to see if the dynamic is similar.
You are on the right track the eddie is the curl of the Momentum energy cP (so-called Dark Energy).
The math is F= XW= [d/dr, DEL] [-vh/l, cP]
Force F = [vp/r -cDEL.P, cdP/dr -DEL vh/l + cDELxP]
Force F = cp/r[v/c -cos(P), – 1P + v/c 1R + sin(P) 1RxP]
Nature has few basic equations and this is the Force Equation.
The curl cDELxP= cp/r sin(P)1RxP is the Polar Jet, perpendicular to plane RxP. The scalar forces Fs=vp/r – cp/r cos(P) determines the rotation angle, cos(X)= Fs/|F|, around the axis Fv.
…
I think that “Mathematically Equivalent” ought to be replaced with more flexible “Physics Equivalent” or even “Engineering Equivalent”.
…