
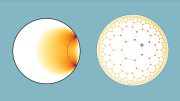
On the left is a representation of a grid of heptagons in a hyperbolic space. To fit the uniform hyperbolic grid into “flat” space, the size and shape of the heptagons are distorted. In the appropriate hyperbolic space, each heptagon would have an identical shape and size, instead of getting smaller and more distorted toward the edges. On the right is a circuit that simulates a similar hyperbolic grid by directing microwaves through a maze of zig-zagging superconducting resonators. Credit: Springer Nature; Produced by Princeton, Houck Lab
Thanks to Einstein, we know that our three-dimensional space is warped and curved. And in curved space, normal ideas of geometry and straight lines break down, creating a chance to explore an unfamiliar landscape governed by new rules. But studying how physics plays out in a curved space is challenging: Just like in real estate, location is everything.
“We know from general relativity that the universe itself is curved in various places,” says JQI Fellow Alicia Kollár, who is also a professor of physics at the University of Maryland (UMD). “But, any place where there’s actually a laboratory is very weakly curved because if you were to go to one of these places where gravity is strong, it would just tear the lab apart.”
Spaces that have different geometric rules than those we usually take for granted are called non-Euclidean. If you could explore non-Euclidean environments, you would find perplexing landscapes. Space might contract so that straight, parallel lines draw together instead of rigidly maintaining a fixed spacing. Or it could expand so that they forever grow further apart. In such a world, four equal-length roads that are all connected by right turns at right angles might fail to form a square block that returns you to your initial intersection.
These environments overturn core assumptions of normal navigation and can be impossible to accurately visualize. Non-Euclidean geometries are so alien that they have been used in video games and horror stories as unnatural landscapes that challenge or unsettle the audience.
But these unfamiliar geometries are much more than just distant, otherworldly abstractions. Physicists are interested in new physics that curved space can reveal, and non-Euclidean geometries might even help improve designs of certain technologies. One type of non-Euclidean geometry that is of interest is hyperbolic space—also called negatively-curved space. Even a two-dimensional, physical version of a hyperbolic space is impossible to make in our normal, “flat” environment. But scientists can still mimic hyperbolic environments to explore how certain physics plays out in negatively curved space.
In a recent paper in Physical Review A, a collaboration between the groups of Kollár and JQI Fellow Alexey Gorshkov, who is also a physicist at the National Institute of Standards and Technology and a Fellow of the Joint Center for Quantum Information and Computer Science, presented new mathematical tools to better understand simulations of hyperbolic spaces. The research builds on Kollár’s previous experiments to simulate orderly grids in hyperbolic space by using microwave light contained on chips. Their new toolbox includes what they call a “dictionary between discrete and continuous geometry” to help researchers translate experimental results into a more useful form. With these tools, researchers can better explore the topsy-turvy world of hyperbolic space.
The situation isn’t precisely like Alice falling down the rabbit hole, but these experiments are an opportunity to explore a new world where surprising discoveries might be hiding behind any corner and the very meaning of turning a corner must be reconsidered.
“There are really many applications of these experiments,” says JQI postdoctoral researcher Igor Boettcher, who is the first author of the new paper. “At this point, it’s unforeseeable what all can be done, but I expect that it will have a lot of rich applications and a lot of cool physics.”
A Curved New World
In flat space, the shortest distance between two points is a straight line, and parallel lines will never intersect—no matter how long they are. In a curved space, these basics of geometry no longer hold true. The mathematical definitions of flat and curved are similar to the day-to-day meaning when applied to two dimensions. You can get a feel for the basics of curved spaces by imagining—or actually playing around with—pieces of paper or maps.
For instance, the surface of a globe (or any ball) is an example of a two-dimensional positively curved space. And if you try to make a flat map into a globe, you end up with excess paper wrinkling up as you curve it into a sphere. To have a smooth sphere you must lose the excess space, resulting in parallel lines eventually meeting, like the lines of longitude that start parallel at the equator meeting at the two poles. Due to this loss, you can think of a positively curved space as being a less-spacy space than flat space.
Hyperbolic space is the opposite of a positively curved space—a more-spacy space. A hyperbolic space curves away from itself at every point. Unfortunately, there isn’t a hyperbolic equivalent of a ball that you can force a two-dimensional sheet into; it literally won’t fit into the sort of space that we live in.
The best you can do is make a saddle (or a Pringle) shape where the surrounding sheet hyperbolically curves away from the center point. Making every point on a sheet similarly hyperbolic is impossible; there isn’t a way to keep curving and adding paper to create a second perfect saddle point without it bunching up and distorting the first hyperbolic saddle point.
The extra space of a hyperbolic geometry makes it particularly interesting since it means that there is more room for forming connections. The differences in the possible paths between points impact how particles interact and what sort of uniform grid—like the heptagon grid shown above—can be made. Taking advantage of the extra connections that are possible in a hyperbolic space can make it harder to completely cut sections of a grid off from each other, which might impact designs of networks like the Internet.
Navigating Labyrinthine Circuits
Since it is impossible to physically make a hyperbolic space on Earth, researchers must settle for creating lab experiments that reproduce some of the features of curved space. Kollár and colleagues previously showed that they can simulate a uniform, two-dimensional curved space. The simulations are performed using circuits (like the one shown above) that serve as a very organized maze for microwaves to travel through.
A feature of the circuits is that microwaves are indifferent to the shapes of the resonators that contain them and are just influenced by the total length. It also doesn’t matter at what angle the different paths connect. Kollár realized that these facts mean the physical space of the circuit can effectively be stretched or squeezed to create a non-Euclidean space—at least as far as the microwaves are concerned.
In their prior work, Kollár and colleagues were able to create mazes with various zig-zagging path shapes and to demonstrate that the circuits simulated hyperbolic space. Despite the convenience and orderliness of the circuits they used, the physics playing out in them still represents a strange new world that requires new mathematical tools to efficiently navigate.
Hyperbolic spaces offer different mathematical challenges to physicists than the Euclidean spaces in which they normally work. For instance, researchers can’t use the standard physicist trick of imagining a lattice getting smaller and smaller to figure out what happens for an infinitely small grid, which should act like a smooth, continuous space. This is because in a hyperbolic space the shape of the lattice changes with its size due to the curving of the space. The new paper establishes mathematical tools, such as a dictionary between discrete and continuous geometry, to circumvent these issues and make sense of the results of simulations.
With the new tools, researchers can get exact mathematical descriptions and predictions instead of just making qualitative observations. The dictionary allows them to study continuous hyperbolic spaces even though the simulation is only of a grid. With the dictionary, researchers can take a description of microwaves traveling between the distinct points of the grid and translate them into an equation describing smooth diffusion, or convert mathematical sums over all the sites on the grid to integrals, which is more convenient in certain situations.
“If you give me an experiment with a certain number of sites, this dictionary tells you how to translate it to a setting in continuous hyperbolic space,” Boettcher says. “With the dictionary, we can infer all the relevant parameters you need to know in the laboratory setup, especially for finite or small systems, which is always experimentally important.”
With the new tools to help understand simulation results, researchers are better equipped to answer questions and make discoveries with the simulations. Boettcher says he’s optimistic about the simulations being useful for investigating the AdS/CFT correspondence, a physics conjecture for combining theories of quantum gravity and quantum field theories using a non-Euclidean description of the universe. And Kollár plans to explore if these experiments can reveal even more physics by incorporating interactions into the simulations.
“The hardware opened up a new door,” Kollár says. “And now we want to see what physics this will let us go to.”
Reference: “Quantum simulation of hyperbolic space with circuit quantum electrodynamics: From graphs to geometry” by Igor Boettcher, Przemyslaw Bienias, Ron Belyansky, Alicia J. Kollár and Alexey V. Gorshkov, 9 September 2020, Physical Review A.
DOI: 10.1103/PhysRevA.102.032208





We extend the results of straight-edged computational geometry into the curved world by defining a pair of new geometric objects, thesplinegon and thesplinehedron, as curved generalizations of the polygon and polyhedron. We identify three distinct techniques for extending polygon algorithms to splinegons: the carrier polygon approach, the bounding polygon approach, and the direct approach. By these methods, large groups of algorithms for polygons can be extended as a class to encompass these new objects. In general, if the original polygon algorithm has time complexityO(f(n)), the comparable splinegon algorithm has time complexity at worstO(Kf(n)) whereK represents a constant number of calls to members of a set of primitive procedures on individual curved edges. These techniques also apply to splinehedra. In addition to presenting the general methods, we state and prove a series of specific theorems. Problem areas include convex hull computation, diameter computation, intersection detection and computation, kernel computation, monotonicity testing, and monotone decomposition, among others.
Another interesting thing about hyperbolic geometry is there is a unit length- an equilateral triangle
This is exciting work!
Not to get too far ahead of the curve; I would think that rather than studying hyperbolic space, studying hyperbolic time would have a more immediate pay off; and, possibly, rather than to think of this universe as a result of a big -bang that that happened once upon a time, but that it’s a probability of what happens whenever there are more more than one possible outcomes; which is to say that all possible outcomes become reality each in its own universe, so in that sense, the big-bang happened just the shortest moment ago, and what the authors described as non-Euclidean geometries, can be described in yet a much infinitely larger universe that can hold an infinite number of universes such as ours; such that, it would in fact be possible to go back in time, kill your mother long before you were ever conceived, come back, and still be able able to live with your mother; you just wouldn’t be exactly in the same universe that you left.