
Something called the fast Fourier transform is running on your cell phone right now. The FFT, as it is known, is a signal-processing algorithm that you use more than you realize. It is, according to the title of one research paper, “an algorithm the whole family can use.”
Alexander Stoytchev – an associate professor of electrical and computer engineering at Iowa State University who’s also affiliated with the university’s Virtual Reality Applications Center, its Human Computer Interaction graduate program, and the department of computer science – says the FFT algorithm and its inverse (known as the IFFT) are at the heart of signal processing.
And, as such, “These are algorithms that made the digital revolution possible,” he said.
They’re a part of streaming music, making a cell phone call, browsing the internet, or taking a selfie.
The FFT algorithm was published in 1965. Four years later, researchers developed a more versatile, generalized version called the chirp z-transform (CZT). But a similar generalization of the inverse FFT algorithm has gone unsolved for 50 years.
Until, that is, Stoytchev and Vladimir Sukhoy – an Iowa State doctoral student co-majoring in electrical and computer engineering, and human-computer interaction – worked together to come up with the long-sought algorithm, called the inverse chirp z-transform (ICZT).
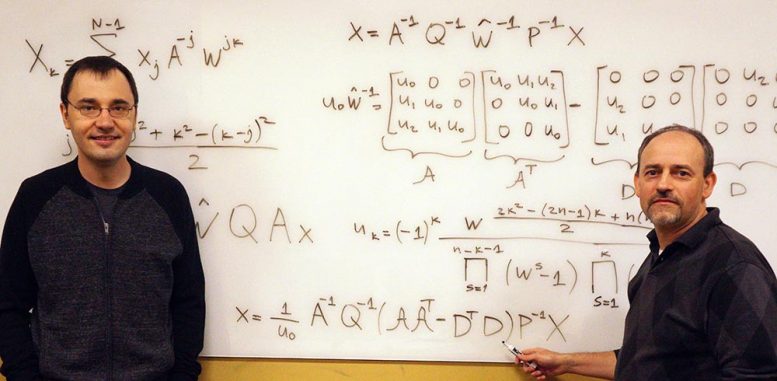
Vladimir Sukhoy and Alexander Stoytchev, left to right, with the derivation for the ICZT algorithm in structured matrix notation — the answer to a 50-year-old puzzle in signal processing. Credit: Photo by Paul Easker
Like all algorithms, it’s a step-by-step process that solves a problem. In this case, it maps the output of the CZT algorithm back to its input. The two algorithms are a little like a series of two prisms – the first separates the wavelengths of white light into a spectrum of colors and the second reverses the process by combining the spectrum back into white light, Stoytchev explained.
Stoytchev and Sukhoy describe their new algorithm in a paper recently published online by Scientific Reports, a Nature Research journal. Their paper shows that the algorithm matches the computational complexity or speed of its counterpart, that it can be used with exponentially decaying or growing frequency components (unlike the IFFT), and that it has been tested for numerical accuracy.
Stoytchev said he stumbled on the idea to attempt to formulate the missing algorithm while looking for analogies to help the graduate students in his “Computational Perception” course understand the fast Fourier transform. He read a lot of the signal-processing literature and couldn’t find anything about the inverse to the related chirp z-transform.
“I got curious,” he said. “Is that because they couldn’t explain it, or is it because it doesn’t exist? It turned out it didn’t exist.”
And so he decided to try to find a fast inverse algorithm.
Sukhoy said the inverse algorithm is a harder problem than the original, forward algorithm and so “we needed better precision and more powerful computers to attack it.” He also said a key was seeing the algorithm within the mathematical framework of structured matrices.
Even then, there were lots of computer test runs “to show everything was working – we had to convince ourselves that this could be done.”
It took courage to keep attacking the problem, said James Oliver, director of Iowa State’s Student Innovation Center and former director of the university’s Virtual Reality Applications Center. Stoytchev and Sukhoy acknowledge Oliver in their paper “for creating the research environment in which we could pursue this work over the past three years.”
Oliver said Stoytchev earned his support for a mathematical and computational challenge that hadn’t been solved for 50 years: “Alex has always impressed me with his passion and commitment to take on big research challenges. There is always risk in research and it takes courage to devote years of hard work to a fundamental problem. Alex is a gifted and fearless researcher.”
Reference: “Generalizing the inverse FFT off the unit circle” by Vladimir Sukhoy and Alexander Stoytchev, 8 October 2019, Scientific Reports.
DOI: 10.1038/s41598-019-50234-9








Be the first to comment on "Engineers Solve 50-Year-Old Puzzle in Signal Processing – Inverse Chirp Z-Transform"