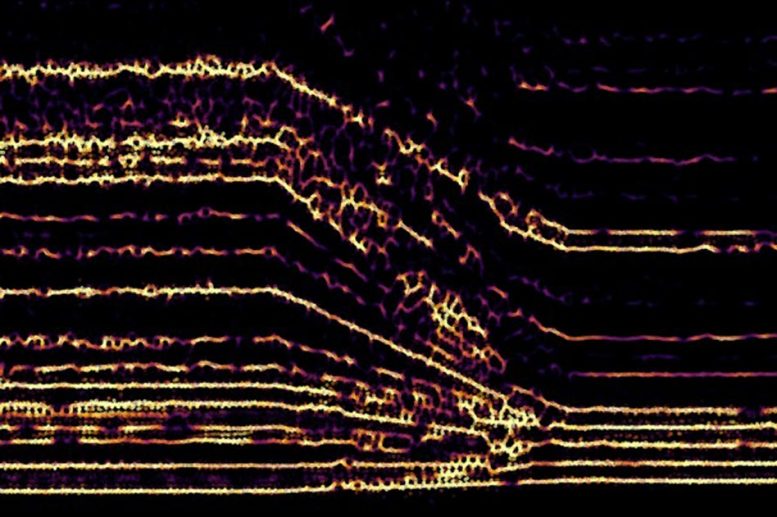
An MIT-invented algorithm automatically produces a “portamento” effect — a pitch sliding from one note to another — between any two audio signals in real time. The algorithm finds the optimal way to move pitches from one signal into another to produce a smooth transition between sounds (shown here). Image courtesy of the researchers
Algorithm enables one audio signal to glide into another, recreating the “portamento” effect of some musical instruments.
In music, “portamento” is a term that’s been used for hundreds of years, referring to the effect of gliding a note at one pitch into a note of a lower or higher pitch. But only instruments that can continuously vary in pitch — such as the human voice, string instruments, and trombones — can pull off the effect.
Now an MIT student has invented a novel algorithm that produces a portamento effect between any two audio signals in real-time. In experiments, the algorithm seamlessly merged various audio clips, such as a piano note gliding into a human voice, and one song blending into another. His paper describing the algorithm won the “best student paper” award at the recent International Conference on Digital Audio Effects.
The algorithm relies on “optimal transport,” a geometry-based framework that determines the most efficient ways to move objects — or data points — between multiple origins and destination configurations. Formulated in the 1700s, the framework has been applied to supply chains, fluid dynamics, image alignment, 3-D modeling, computer graphics, and more.
In work that originated in a class project, Trevor Henderson, now a graduate student in computer science, applied optimal transport to interpolating audio signals — or blending one signal into another. The algorithm first breaks the audio signals into brief segments. Then, it finds the optimal way to move the pitches in each segment to pitches in the other signal, to produce the smooth glide of the portamento effect. The algorithm also includes specialized techniques to maintain the fidelity of the audio signal as it transitions.
“Optimal transport is used here to determine how to map pitches in one sound to the pitches in the other,” says Henderson, a classically trained organist who performs electronic music and has been a DJ on WMBR 88.1, MIT’s radio station. “If it’s transforming one chord into a chord with a different harmony, or with more notes, for instance, the notes will split from the first chord and find a position to seamlessly glide to in the other chord.”
According to Henderson, this is one of the first techniques to apply optimal transport to transforming audio signals. He has already used the algorithm to build equipment that seamlessly transitions between songs on his radio show. DJs could also use the equipment to transition between tracks during live performances. Other musicians might use it to blend instruments and voices on stage or in the studio.

Trevor Henderson in the record library at WMBR, MIT’s student radio station. Credit: Melanie Gonick, MIT
Henderson’s co-author on the paper is Justin Solomon, an X-Consortium Career Development Assistant Professor in the Department of Electrical Engineering and Computer Science. Solomon — who also plays cello and piano — leads the Geometric Data Processing Group in the Computer Science and Artificial Intelligence Laboratory (CSAIL) and is a member of the Center for Computational Engineering.
Henderson took Solomon’s class, 6.838 (Shape Analysis), which tasks students with applying geometric tools like optimal transport to real-world applications. Student projects usually focus on 3-D shapes from virtual reality or computer graphics. So Henderson’s project came as a surprise to Solomon. “Trevor saw an abstract connection between geometry and moving frequencies around in audio signals to create a portamento effect,” Solomon says. “He was in and out of my office all semester with DJ equipment. It wasn’t what I expected to see, but it was pretty entertaining.”
For Henderson, it wasn’t too much of a stretch. “When I see a new idea, I ask, ‘Is this applicable to music?’” he says. “So, when we talked about optimal transport, I wondered what would happen if I connected it to audio spectra.”
A good way to think of optimal transport, Henderson says, is finding “a lazy way to build a sand castle.” In that analogy, the framework is used to calculate the way to move each grain of sand from its position in a shapeless pile into a corresponding position in a sand castle, using as little work as possible. In computer graphics, for instance, optimal transport can be used to transform or morph shapes by finding the optimal movement from each point on one shape into the other.
Applying this theory to audio clips involves some additional ideas from signal processing. Musical instruments produce sound through vibrations of components, depending on the instrument. Violins use strings, brass instruments use air inside hollow bodies, and humans use vocal cords. These vibrations can be captured as audio signals, where the frequency and amplitude (peak height) represent different pitches.
Conventionally, the transition between two audio signals is done with a fade, where one signal is reduced in volume while the other rises. Henderson’s algorithm, on the other hand, smoothly slides frequency segments from one clip into another, with no fading of volume.
To do so, the algorithm splits any two audio clips into windows of about 50 milliseconds. Then, it runs a Fourier transform, which turns each window into its frequency components. The frequency components within a window are lumped together into individual synthesized “notes.” Optimal transport then maps how the notes in one signal’s window will move to the notes in the other.
Then, an “interpolation parameter” takes over. That’s basically a value that determines where each note will be on the path from its starting pitch in one signal to its ending pitch in the other. Manually changing the parameter value will sweep the pitches between the two positions, producing the portamento effect. That single parameter can also be programmed into and controlled by, say, a crossfader, a slider component on a DJ’s mixing board that smoothly fades between songs. As the crossfader slides, the interpolation parameter changes to produce the effect.
Behind the scenes are two innovations that ensure a distortion-free signal. First, Henderson used a novel application of a signal-processing technique, called “frequency reassignment,” that lumps the frequency bins together to form single notes that can easily transition between signals. Second, he invented a way to synthesize new phases for each audio signal while stitching together the 50-millisecond windows, so neighboring windows don’t interfere with each other.
Next, Henderson wants to experiment with feeding the output of the effect back into its input. This, he thinks, could automatically create another classic music effect, “legato,” which is a smooth transition between distinct notes. Unlike a portamento — which plays all notes between a start and end note — a legato seamlessly transitions between two distinct notes, without capturing any notes in between.
Reference: “Audio Transport: A Generalized Portamento via Optimal Transport” by Trevor Henderson, 16 June 2019, The 22nd International Conference on Digital Audio Effects. (PDF)
DOI: 10.48550/arXiv.1906.06763








Be the first to comment on "Algorithm Uses Math to Blend Musical Notes Seamlessly [Video]"