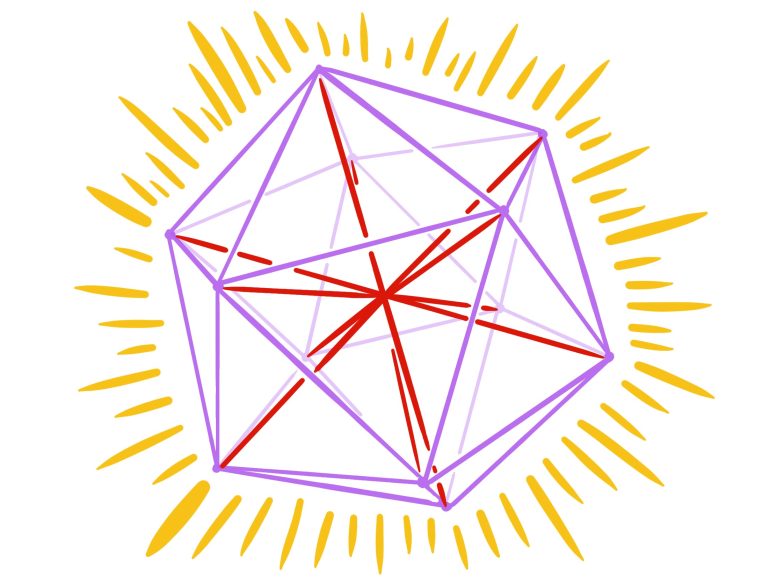
In a regular icosahedron (purple), six main interior diagonals (red lines) make equal angles with each other. Credit: Image: Zilin Jiang
How many lines can be pairwise separated by the same angle in high dimensions? Geometry breakthrough gives new insights into spectral graph theory.
Equiangular lines are lines in space that pass through a single point, and whose pairwise angles are all equal. Picture in 2D the three diagonals of a regular hexagon, and in 3D, the six lines connecting opposite vertices of a regular icosahedron (see the figure above). Mathematicians are not limited to three dimensions, however.
“In high dimensions, things really get interesting, and the possibilities can seem limitless,” says Yufei Zhao, assistant professor of mathematics.
But they aren’t limitless, according to Zhao and his team of MIT mathematicians, who sought to solve this problem on the geometry of lines in high-dimensional space. It’s a problem that researchers have been puzzling over for at least 70 years.
Their breakthrough determines the maximum possible number of lines that can be placed so that the lines are pairwise separated by the same given angle. Zhao wrote the paper with a group of MIT researchers consisting of undergraduates Yuan Yao and Shengtong Zhang, PhD student Jonathan Tidor, and postdoc Zilin Jiang. (Yao recently started as an MIT math PhD student, and Jiang is now a faculty member at Arizona State University). Their paper will be published in the January 2022 issue of Annals of Mathematics.

“The proof worked out cleanly and beautifully,” says Yufei Zhao (center). “We had so much fun working on this problem together.” Left to right: Zilin Jiang, Jonathan Tidor, Zhao, Yuan Yao, and Shengtong Zhang. Credit: Photo: Sandi Miller/MIT Department of Mathematics
The mathematics of equiangular lines can be encoded using graph theory. The paper provides new insights into an area of mathematics known as spectral graph theory, which provides mathematical tools for studying networks. Spectral graph theory has led to important algorithms in computer science such as Google’s PageRank algorithm for its search engine.
This new understanding of equiangular lines has potential implications for coding and communications. Equiangular lines are examples of “spherical codes,” which are important tools in information theory, allowing different parties to send messages to each other over a noisy communication channel, such as those sent between NASA and its Mars rovers.
The problem of studying the maximum number of equiangular lines with a given angle was introduced in a 1973 paper of P.W.H. Lemmens and J.J. Seidel.
“This is a beautiful result providing a surprisingly sharp answer to a well-studied problem in extremal geometry that received a considerable amount of attention starting already in the ’60s,” says Princeton University professor of mathematics Noga Alon.
The new work by the MIT team provides what Zhao calls “a satisfying resolution to this problem.”
“There were some good ideas at the time, but then people got stuck for nearly three decades,” Zhao says. There was some important progress made a few years ago by a team of researchers including Benny Sudakov, a professor of mathematics at the Swiss Federal Institute of Technology (ETH) Zurich. Zhao hosted Sudakov’s visit to MIT in February 2018 when Sudakov spoke in the combinatorics research seminar about his work on equiangular lines.
Jiang was inspired to work on the problem of equiangular lines based on the work of his former PhD advisor Bukh Boris at Carnegie Mellon University. Jiang and Zhao teamed up in the summer of 2019, and were joined by Tidor, Yao, and Zhang. “I wanted to find a good summer research project, and I thought that this was a great problem to work on,” Zhao explains. “I thought we might make some nice progress, but it was definitely beyond my expectations to completely solve the entire problem.”
The research was partially supported by the Alfred P. Sloan Foundation and the National Science Foundation. Yao and Zhang participated in the research through the Department of Mathematics’ Summer Program for Undergraduate Research (SPUR), and Tidor was their graduate student mentor. Their results had earned them the mathematics department’s Hartley Rogers Jr. Prize for the best SPUR paper.
“It is one of the most successful outcomes of the SPUR program,” says Zhao. “It’s not every day that a long-standing open problem gets solved.”
One of the key mathematical tools used in the solution is known as spectral graph theory. Spectral graph theory tells us how to use tools from linear algebra to understand graphs and networks. The “spectrum” of a graph is obtained by turning a graph into a matrix and looking at its eigenvalues.
“It is as if you shine an intense beam of light on a graph and then examine the spectrum of colors that come out,” Zhao explains. “We found that the emitted spectrum can never be too heavily concentrated near the top. It turns out that this fundamental fact about the spectra of graphs has never been observed.”
The work gives a new theorem in spectral graph theory — that a bounded degree graph must have sublinear second eigenvalue multiplicity. The proof requires clever insights relating the spectrum of a graph with the spectrum of small pieces of the graph.
“The proof worked out cleanly and beautifully,” Zhao says. “We had so much fun working on this problem together.”
Reference: “Equiangular lines with a fixed angle” by Zilin Jiang, Jonathan Tidor, Yuan Yao, Shengtong Zhang and Yufei Zhao, November 2021, Annals of Mathematics.
DOI: 10.4007/annals.2021.194.3.3
arXiv:1907.12466






Be the first to comment on "MIT Mathematicians Solve an Old Geometry Problem on Equiangular Lines"