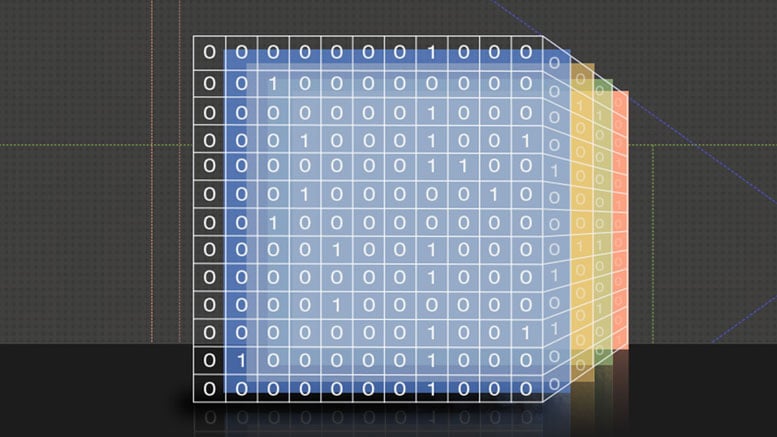
A new compiler developed by MIT makes complex sparse matrix and tensor computations easy and generates highly efficient code automatically.
A new MIT computer system speeds computations involving “sparse tensors,” multidimensional data arrays that consist mostly of zeroes.
At the Association for Computing Machinery’s Conference on Systems, Programming, Languages and Applications: Software for Humanity (SPLASH), researchers from MIT, the French Alternative Energies and Atomic Energy Commission, and Adobe Research recently presented a new system that automatically produces code optimized for sparse data.
We live in the age of big data, but most of that data is “sparse.” Imagine, for instance, a massive table that mapped all of Amazon’s customers against all of its products, with a “1” for each product a given customer bought and a “0” otherwise. The table would be mostly zeroes.
With sparse data, analytic algorithms end up doing a lot of addition and multiplication by zero, which is wasted computation. Programmers get around this by writing custom code to avoid zero entries, but that code is complex, and it generally applies only to a narrow range of problems.
The new code offers a 100-fold speedup over existing, non-optimized software packages. And its performance is comparable to that of meticulously hand-optimized code for specific sparse-data operations, while requiring far less work on the programmer’s part.
The system is called Taco, for tensor algebra compiler. In computer-science parlance, a data structure like the Amazon table is called a “matrix,” and a tensor is just a higher-dimensional analogue of a matrix. If that Amazon table also mapped customers and products against the customers’ product ratings on the Amazon site and the words used in their product reviews, the result would be a four-dimensional tensor.
“Sparse representations have been there for more than 60 years,” says Saman Amarasinghe, an MIT professor of electrical engineering and computer science (EECS) and senior author on the new paper. “But nobody knew how to generate code for them automatically. People figured out a few very specific operations — sparse matrix-vector multiply, sparse matrix-vector multiply plus a vector, sparse matrix-matrix multiply, sparse matrix-matrix-matrix multiply. The biggest contribution we make is the ability to generate code for any tensor-algebra expression when the matrices are sparse.”
Joining Amarasinghe on the paper are first author Fredrik Kjolstad, an MIT graduate student in EECS; Stephen Chou, also a graduate student in EECS; David Lugato of the French Alternative Energies and Atomic Energy Commission; and Shoaib Kamil of Adobe Research.
Custom kernels
In recent years, the mathematical manipulation of tensors — tensor algebra — has become crucial to not only big-data analysis but machine learning, too. And it’s been a staple of scientific research since Einstein’s time.
Traditionally, to handle tensor algebra, mathematics software has decomposed tensor operations into their constituent parts. So, for instance, if a computation required two tensors to be multiplied and then added to a third, the software would run its standard tensor multiplication routine on the first two tensors, store the result, and then run its standard tensor addition routine.
In the age of big data, however, this approach is too time-consuming. For efficient operation on massive data sets, Kjolstad explains, every sequence of tensor operations requires its own “kernel,” or computational template.
“If you do it in one kernel, you can do it all at once, and you can make it go faster, instead of having to put the output in memory and then read it back in so that you can add it to something else,” Kjolstad says. “You can just do it in the same loop.”
Computer science researchers have developed kernels for some of the tensor operations most common in machine learning and big-data analytics, such as those enumerated by Amarasinghe. But the number of possible kernels is infinite: The kernel for adding together three tensors, for instance, is different from the kernel for adding together four, and the kernel for adding three three-dimensional tensors is different from the kernel for adding three four-dimensional tensors.
Many tensor operations involve multiplying an entry from one tensor with one from another. If either entry is zero, so is their product, and programs for manipulating large, sparse matrices can waste a huge amount of time adding and multiplying zeroes.
Hand-optimized code for sparse tensors identifies zero entries and streamlines operations involving them — either carrying forward the nonzero entries in additions or omitting multiplications entirely. This makes tensor manipulations much faster, but it requires the programmer to do a lot more work.
The code for multiplying two matrices — a simple type of tensor, with only two dimensions, like a table — might, for instance, take 12 lines if the matrix is full (meaning that none of the entries can be omitted). But if the matrix is sparse, the same operation can require 100 lines of code or more, to track omissions and elisions.
Enter Taco
Taco adds all that extra code automatically. The programmer simply specifies the size of a tensor, whether it’s full or sparse, and the location of the file from which it should import its values. For any given operation on two tensors, Taco builds a hierarchical map that indicates, first, which paired entries from both tensors are nonzero and, then, which entries from each tensor are paired with zeroes. All pairs of zeroes it simply discards.
Taco also uses an efficient indexing scheme to store only the nonzero values of sparse tensors. With zero entries included, a publicly released tensor from Amazon, which maps customer ID numbers against purchases and descriptive terms culled from reviews, takes up 107 exabytes of data, or roughly 10 times the estimated storage capacity of all of Google’s servers. But using the Taco compression scheme, it takes up only 13 gigabytes — small enough to fit on a smartphone.
“Many research groups over the last two decades have attempted to solve the compiler-optimization and code-generation problem for sparse-matrix computations but made little progress,” says Saday Sadayappan, a professor of computer science and engineering at Ohio State University, who was not involved in the research. “The recent developments from Fred and Saman represent a fundamental breakthrough on this long-standing open problem.”
“Their compiler now enables application developers to specify very complex sparse matrix or tensor computations in a very easy and convenient high-level notation, from which the compiler automatically generates very efficient code,” he continues. “For several sparse computations, the generated code from the compiler has been shown to be comparable or better than painstakingly developed manual implementations. This has the potential to be a real game-changer. It is one of the most exciting advances in recent times in the area of compiler optimization.”
Reference: “The Tensor Algebra Compiler” by Fredrik Kjolstad, Shoaib Kamil, Stephen Chou, David Lugato and Saman Amarasinghe, 12 October 2017, Proceedings of the ACM on Programming Languages.
DOI: 10.1145/3133901
PDF







Be the first to comment on "New System for Performing “Tensor Algebra” Offers Faster Big-Data Analysis"