
Luminous defects: Nitrogen dopants in a diamond can be excited with green light so that the gemstone glows red. The diamond which the Stuttgart-based researchers use for their experiments contains very few nitrogen defects. At a single one of these defects, a so-called NV center, the researchers produce a quantum register, where they demonstrate the error correction on a quantum bit. Credit: Universität Stuttgart
An international team of physicists has discovered a way to control the quantum system of a diamond with a small number of nitrogen impurities.
Computers do not necessarily have to perform error-free calculations in order to provide perfect results – they only need to correct their errors in a reliable way. And this will become even more important in the future, when it is hoped that quantum computers will solve some tasks several times faster than conventional PCs with computing processes that are very efficient but also prone to disturbances. An international team headed by physicists from the University of Stuttgart and the Stuttgart Max Planck Institute for Solid State Research has now found a way to control the quantum system of a diamond with a small number of nitrogen impurities particularly well. The researchers can thus specifically address quantum bits, i.e. the smallest computing units of a quantum computer, in the diamond and combine several bits to a computing register. They use the new degree of control for a logic operation, which is essential for a quantum computer, and for error correction.
The physicists already possess quite accurate knowledge about where the strengths of a quantum computer would be: it could carry out searches in large databases, encodings, and decodings, or the research tasks in quantum physics much faster than any conceivable conventional computer today. However, there is still no really clear idea of what the blueprint of a quantum computer should look like; neither is there currently a real favorite among the materials from which quantum processors could be made. Possible options here are ions trapped by electric fields, atoms in optical lattices, devices made of superconductors, or diamonds doped with tiny quantities of nitrogen, for example.
Physicists working with Jörg Wrachtrup, professor at the University of Stuttgart and Fellow of the Max Planck Institute for Solid State Research, have been investigating for some time the diamonds which are sporadically interspersed with nitrogen. On the road to the quantum computer, they have now helped the diamonds over several hurdles simultaneously. The Stuttgart-based researchers did this by producing not only a quantum register and thus the counterpart of a conventional processor in a diamond; they were also able to reliably control the register, use it to carry out a logic operation, and correct errors in it. “Since we meanwhile understand the quantum mechanics of our system well, we can produce quantum registers using a quite simple approach that doesn’t require complex cryogenic technology or laser systems,” says Jörg Wrachtrup.
A quantum register is in a superposition state of several qubits
A quantum register always contains individual qubits (short for quantum bits), which can be in one of two states just like conventional bits in order to represent a zero or a one. Unlike conventional bits, however, several qubits can be brought into superposition states in which every individual bit virtually floats between “zero” and “one”. This means each superposition state has a different occurrence and these are contained in the quantum register as possibilities. These possibilities can be used like the bits of a conventional computer for some parallel computations.
The more quantum bits are combined in a register, the more powerful, but also the more sensitive, is the processor. This is because external disturbances push a qubit only too easily from the floating state between “one” and “zero” towards one of the two options. In the worst case, unwelcome external influences destroy the sensitive superposition and render it useless for parallel computations. The researchers in Stuttgart have now found a remedy for this.
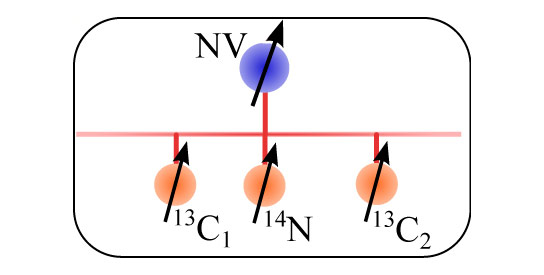
Schematic of the quantum register: Via the interaction (red lines) with the spin of the electron (blue) in an NV center and radio pulses the nuclear spins of atoms (orange) in the vicinity of the NV center can be controlled – here the nuclear spins of a nitrogen atom and two carbon atoms of the heavy isotope 13C. Each spin is indicated by an arrow. Credit: Nature; doi:10.1038/nature12919
Three nuclear spins are combined to a quantum register via a defect
They use two carbon atoms of the heavy C13 isotope and one nitrogen atom as the quantum bits. These atoms each have a nuclear spin which can adopt two orientations in a magnetic field and can be manipulated by means of radio frequency pulses. The orientation of the nuclear spin provides views into the human body in nuclear magnetic resonance tomography; however, in the qubit it is used to file the “zero” or “one” of a bit. The only thing now missing is a control unit to allow the Stuttgart-based researchers to control the quantum bits and combine them into a register. This is where the irregularity in the atomic lattice of the diamond, which is caused by the nitrogen atom, comes into play.
The nitrogen defect – physicists call it an NV center (NV: nitrogen vacancy) – can become a trap for one single electron. An electron also has a spin whose orientation also has an effect on the orientation of the nuclear spin. The electron spin can be switched faster than the nuclear spins, but is more prone to the effect of disturbances. The researchers use it for control commands to the nuclear spins that cannot be transmitted with radio frequency pulses. The electron in the defect thus provides the communication between the nuclear spins in the quantum register. Finally, the physicists use it as a tool to help them read the nuclear spins.
A quantum register with fast switch and robust storage device
“In the past, the electron of the NV center has been used as a storage device in order to expand the quantum register,” says Gerald Waldherr, who played a crucial role in the experiments. “We use the electron solely to control the nuclear spins on which the quantum information is stored.” This allows the researchers to use the advantages of both systems: the quantum register can be switched rapidly using an electron spin. The nuclear spins, in contrast, store the information in a relatively reliable way, as they withstand disturbances well.
Assisted by the electron spin, the physicists now use an ingenious combination of light and radio frequency pulses to manipulate the three nuclear spins into a superposition state initially: they entangle the nuclear spins. Quantum mechanical entanglement creates a kind of virtual bond between quantum particles so that they know of each other’s existence. Only entangled systems are suitable as quantum registers, because only they allow the parallel operation of the quantum computer.
A CNOT gate allows other computing operations
In the next step, the researchers showed that logic operations are possible in this quantum register using a CNOT gate – a logic operation that is particularly important for quantum computers. “All other operations can be realized with the CNOT gate and local operations on individual qubits,” explains Gerald Waldherr. The CNOT gate switches a bit depending on a second bit. If the latter represents a “one”, for example, the first one is set from “zero” to “one” or vice versa; it remains unchanged, however, if the latter is at “zero”. The researchers in Stuttgart carried out exactly this operation on the nuclear spins in their register, by sending a sequence of different radio frequency pulses to the NV center or the nuclear spins.

Complete control over a quantum register: The physicists from the University of Stuttgart and the Max Planck Institute for Solid State Research fix an almost square diamond measuring four millimeters long and wide and one millimeter high onto a gold substrate. They address the electron of an individual nitrogen defect (NV center) with green laser light. Two strip-like cuts in the gold foil create a narrow conductive track which leads to the NV center. This track is used to generate radio frequency pulses to manipulate the individual nuclear spins. Credit: Gerald Waldherr
The CNOT gate is not only indispensable for the computing power of a quantum computer, it also makes error correction possible. Although nuclear spins are not as sensitive to interferences as electron spins are, they are by no means immune. Gerald Waldherr and his colleagues demonstrated how possible errors in the quantum register can be canceled for one of the possible superposition states of their quantum register.
To correct the errors, the scientists benefit from the fact that the superposition states are not arbitrary combinations of all possible spin orientations. Rather, in one of these superposition states all qubits are either “one” or “zero”. In another state, two are always “one”. Errors are thus evident immediately. And with the aid of the two intact qubits the original state of the third can be reconstructed. The CNOT operation is the tool of choice for this, because it switches one bit depending on another one. An ingenious sequence of CNOT operations on the three qubits of the quantum register thus not only shows whether one bit deviates from the characteristic pattern of the particular superposition state, it even corrects the error immediately.
The plan is to increase the number of qubits in the quantum register
“Our current work shows that the defect centers in diamonds are significantly more versatile than we originally thought,” says Jörg Wrachtrup. “We have obtained the new findings primarily through a better understanding of the defects and not by investing much into the material.”
The researchers will rely on smart ideas in the future as well, as they try to further improve the prospects of the diamonds in the competition for the most useful quantum register. First, they want to increase the number of qubits in their register. To this end, they want to integrate nuclear spins, which find it more difficult to communicate with the electron than the three spins of their current computing register. They could also expand the quantum register, if they succeed in entangling several NV centers and addressing the relevant nuclear spins in the vicinity of the individual centers. They would thus also have networked the nuclear spins, which are controlled by the individual defects. The quantum register would then slowly be approaching a size where it could actually challenge conventional processors for some computing tasks.
Reference: “Quantum error correction in a solid-state hybrid spin register” by G. Waldherr, Y. Wang, S. Zaiser, M. Jamali, T. Schulte-Herbrüggen, H. Abe, T. Ohshima, J. Isoya, J. F. Du, P. Neumann and J. Wrachtrup, 12 February 2014, Nature.
DOI: 10.1038/nature12919
arXiv:1309.6424








One point that may be helpful in clarifying what the scientists are doing would be to distinguish between logical and physical qubits. One entangles physical qubits that are individually unreliable into logical qubits that, thanks to a redundancy between the physical qubits are more reliable.
That is, the combined state is α |0>|0>|0> + β |1>|1>|1> (or with greater brevity, α |000> + β |111>) in order to construct the logical qubit α |0> + β |1> and the coefficients α and β are complex numbers, such that is neither |0> nor |1> but a linear combination of the two that when measured may give probabilistic mixture of |0>s and |1>s, or in terms of the physical qubits, assuming there are no errors in the third, |000> or |111>. The probabilities are proportional to the squares of the absolute values of the coefficients α and β, respectively. The three physical qubits act as a double or more accurately, triple check on each other.
If qubits are limited to states of 0 or 1 then there is no quantum advantage. Non-quantum computers (either deterministic or probabilistic) can efficiently model such quantum computation. Likewise, if there is no destructive interference (i.e., a probabilistic Turing machine), or for that matter, the logical qubits are too highly entangled.
Many quantum algorithms make considerable use of Bell states that are created by means of Hadamard gates, and such states are ones in which measurements will return either 0 or 1 with equal probability. This is necessary for quantum parallelism as it is what makes possible the exploration of all combinations of zeros and ones at the same time.
As the author of this article and authors of this paper state, they are working with qubits that are in states of linear combination of the computational basis vectors, that is in superposition:
“The original state |ψ> = α |0> + β |1> is encoded as α |y+y+y+> + β |y−y−y−>. After decoding, the state will be α |000> + β |111> in case of no error, and α |001> + β |110> in case of an error on e.g. 13C2. Then, the error is detected by the other two qubits, by flipping them conditional on the state of 13C2, yielding |00> ⊗ (α |0> + β |1>) and |11> ⊗ (α |1> + β |0>), respectively.”
… and likewise,
“In the following, we illustrate the mechanism on the creation of a two qubit GHZ-like state using a nuclear CPhase gate based on a conditional 2πx rotation of the electron spin. We start with both nuclear qubits initialized in state |00>, and apply πx/2 rotations on both, to end up in (excluding normalization)
|00> − i|01> − |10> + i|11>. (1)
Normalization in this case would be by division of 2.
This is, however, at least in principle, fully deterministic until the point of measurement. Vectors representing either qubit states or multi-qubit combinations of qubit states are rotated in a complex number, many dimensional Hilbert space in which the number of dimensions increases exponentially as a function of the number of qubits, in which each dimension corresponds to one possible combination of the measurement values of logical qubits, and where gates perform well-defined rotations in this space until the point of measurement. Moreover, since the Hadamard gate is its own inverse it is possible to return the qubits back to a zero or one with a probability of 1.
More broadly though, the coefficients associated with each possible combination of logical qubits are each able to vary almost independently of the rest. The only absolute constraint is that the length of the vector in Hilbert space is 1. As such, typically quantum algorithms give probabilistic results. The trick in such cases is to design them such that the probability of obtaining the right answer is as close to 1 as possible. In many of these algorithms this is done through a process of repeating a sequence of steps that amplify the probability of obtaining that answer. Grover’s algorithm for searching an unstructured database is a good case in point.
PS
My apologies… I didn’t notice the date when I first read the article and commented. Normally people don’t comment so long after a story has been posted and I try to abide by that rule. Regardless, I really like the article, and I see that there are a fair number of articles on quantum computation at this site. Looking forward to reading them and those yet to come. And, as in this case, I greatly appreciate the link to the tech paper. Thank you!
good thank you
32:42
David Bohm Interview on Non-Local Quantum Mechanics 1989
… qubit states or multi-qubit combinations of qubit states are rotated in a complex number the measurement values of logical algorithms, which is done through a process of repeating sequential cross-variables, steps that amplify the probability of obtaining criterion on the basis of the algorithms turns… Grover’s algorithm for searching an unstructured database is a good case to reference Bohm . . .
(Quantum algorithms give probabilistic results.)
If the electron is bisecting the space its potential occupies, where is the integument?
quantum work field empirical electron
Google Images