
After two decades, researchers found a gamma-ray “mystery source”: a neutron star with a low-mass companion.
Super Heavyweight and Flyweight in a Cosmic Dance
Volunteer distributed computing project Einstein@Home discovers neutron star in unusual binary system.
After more than two decades, an international research team led by the Max Planck Institute for Gravitational Physics (Albert Einstein Institute; AEI) in Hannover has identified a Galactic “mystery source” of gamma rays: a heavy neutron star with a very low mass companion orbiting it. Using novel data analysis methods running on about 10,000 graphics cards in the distributed computing project Einstein@Home, the team identified the neutron star by its regularly pulsating gamma rays in a deep search of data from NASA’s Fermi satellite. Surprisingly, the neutron star is completely invisible in radio waves. The binary system was characterized with an observing campaign across the electromagnetic spectrum, and breaks several records.
An odd couple sets new records
“The binary star system and the neutron star at its heart, now known as PSR J1653-0158, set new records,” explains Lars Nieder, PhD student at the AEI Hannover and first author of the study published today in Astrophysical Journal Letters. “We have discovered the Galactic dance of a super heavyweight with a flyweight: At slightly more than twice the mass of our Sun, the neutron star is extraordinarily heavy. Its companion has about six times the density of lead, but only about 1% the mass of our Sun. This ‘odd couple’ orbits every 75 minutes, more quickly than all known comparable binaries.”

Illustration of the binary star system with the pulsar J1653-0158 (bottom) in comparison to the Earth-Moon system (top). All objects and orbits are shown to scale except for the pulsar, which is magnified 450 times. The binary star system with an orbital period of only 75 minutes is only slightly larger than the Earth-Moon system. Credit: Knispel/Clark/Max Planck Institute for Gravitational Physics/NASA
The neutron star also spins around its own axis at more than 30,000 rpm, making it one of the fastest rotating. At the same time, its magnetic field – usually extremely strong in neutron stars – is exceptionally weak. This record discovery was enabled by two important steps.
Step 1: Observing at many wavelengths
Astronomical observations from 2014 made it possible to determine the properties of the binary star’s orbits.
“That a neutron star is behind the gamma-ray source known since 1999 was considered probable since 2009. In 2014 after observations of the system with optical and X-ray telescopes it became clear that this is a very tight binary system. But all searches for the neutron star in it have so far been in vain,” says Dr. Colin Clark of the Jodrell Bank Centre for Astrophysics, co-author of the study and former PhD student at AEI Hannover.
Step 2: Harnessing computational power donated to Einstein@Home
To unambiguously prove the existence of a neutron star, not just its radio waves or gamma rays, but also their characteristic pulsations must be detected. The rotation of the neutron star causes this regular flashing, similar to the periodic twinkling of a distant lighthouse. The neutron star is then called a radio or gamma-ray pulsar, respectively.
“In binary systems like the one we have now discovered, pulsars are known as ‘black widows’ because, like spiders of the same name, they eat their partners, so to speak,” explains Clark. He adds: “The pulsar vaporizes its companion with its radiation and a particle wind, filling the star system with plasma that is impenetrable to radio waves.”
Gamma rays, on the other hand, are not stopped by these plasma clouds. The Large Area Telescope (LAT) on board NASA’s Fermi Gamma-ray Space Telescope detects this radiation.
The team used the 2014 data, further observations with the William Herschel Telescope on La Palma, and the precise sky position determined by the Gaia satellite to target and focus the computing power of the volunteer distributed computing project Einstein@Home. This also provided a more complete sketch of the companion star.
Finding a very close binary system with improved analysis
Improving on earlier methods developed for this purpose, they enlisted the help of tens of thousands of volunteers to search about a decade of archival data from the Fermi LAT for periodic pulsations. The volunteers donated idle compute cycles on the graphics cards (GPUs) of their computers to Einstein@Home. In less than two weeks, the team made a discovery that would have taken centuries of computing time on a conventional computer.
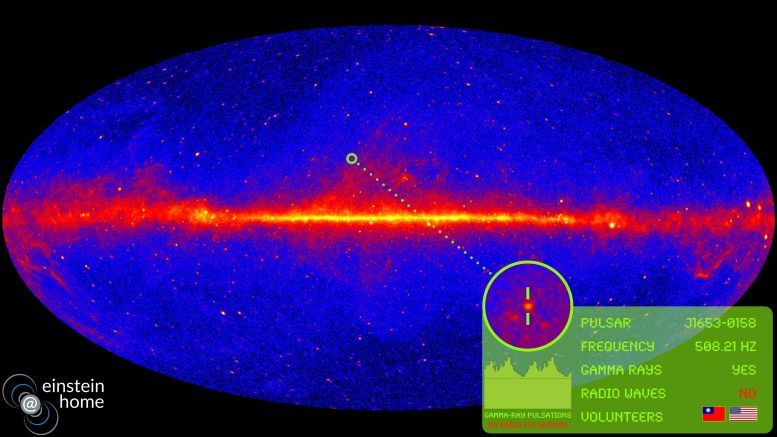
The entire sky as seen by the Fermi Gamma-ray Space Telescope and the new pulsar discovered by Einstein@Home. The field below the magnified inset shows the pulsar name and some of its measured characteristics, as well as its gamma-ray pulsations. The flags show the nationalities of the volunteers whose computers found the pulsar. Credit: Knispel/Max Planck Institute for Gravitational Physics/NASA/DOE/Fermi LAT Collaboration
“We have found a very tight binary system. In its center is the pulsar, which is about 20 kilometers in size and has twice the mass of our Sun. The remnant of a dwarf star orbits the pulsar at just 1.3 times the Earth-Moon distance in only 75 minutes at a speed of more than 700 kilometers per second,” explains Nieder. “This unusual duo might have originated from an extremely close binary system, in which matter originally flowed from the companion star onto the neutron star, increasing its mass and causing it to rotate faster and faster while simultaneously dampening its magnetic field.”
Searching for radio and gravitational waves
After identifying the gamma-ray pulsar, the team used their newly gained knowledge and searched again for its radio waves. They found no trace, although they used the largest and most sensitive radio telescopes in the world. PSR J1653-0158 thus becomes the second rapidly rotating pulsar from which no radio waves are seen. There are two possible explanations: Either the pulsar sends no radio waves towards Earth, or, more likely, the plasma cloud envelops the binary star system so completely that no radio waves reach Earth.
In a further step, they searched data from the first and second observing runs of the Advanced LIGO detectors for possible gravitational waves that the neutron star would emit if it were slightly deformed. Again, the search was unsuccessful.
Exciting future
“In the catalog of gamma-ray sources found by the Fermi satellite, there are dozens more that I would bet have binary pulsars in them,” says Prof. Bruce Allen, Director at the Max Planck Institute for Gravitational Physics in Hannover and Director and founder of Einstein@Home. “But so far no one has been able to detect the characteristic pulsation of their gamma rays. With Einstein@Home, we hope do just that — who knows what other surprises await us.”
Reference: “Discovery of a Gamma-Ray Black Widow Pulsar by GPU-accelerated Einstein@Home” by L. Nieder, C. J. Clark, D. Kandel, R. W. Romani, C. G. Bassa, B. Allen, A. Ashok, I. Cognard, H. Fehrmann, P. Freire, R. Karuppusamy, M. Kramer, D. Li, B. Machenschalk, Z. Pan, M. A. Papa, S. M. Ransom, P. S. Ray, J. Roy, P. Wang, J. Wu, C. Aulbert, E. D. Barr, B. Beheshtipour, O. Behnke, B. Bhattacharyya, R. P. Breton, F. Camilo, C. Choquet, V. S. Dhillon, E. C. Ferrara, L. Guillemot, J. W. T. Hessels, M. Kerr, S. A. Kwang, T. R. Marsh, M. B. Mickaliger, Z. Pleunis, H. J. Pletsch, M. S. E. Roberts, S. Sanpa-arsa and B. Steltner, 22 October 2020, The Astrophysical Journal Letters.
DOI: 10.3847/2041-8213/abbc02
Background information
Who made the discovery? The discovery was enabled by tens of thousands of Einstein@Home volunteers who have donated their CPU and GPU time to the project. Without them, this study could not have been performed and this discovery could not have been made. The team is especially grateful to those volunteers whose computers discovered the pulsar: Yi-Sheng Wu of Taoyuan, Taiwan and Daniel Scott of Ankeny, Iowa, USA.
Neutron stars are compact remnants from supernova explosions and consist of exotic, extremely dense matter. They measure about 20 kilometers across and weigh more than our Sun. Because of their strong magnetic fields and fast rotation they emit beamed radio waves and energetic gamma rays similar to a cosmic lighthouse. If these beams point towards Earth during the neutron star’s rotation, it becomes visible as a pulsating radio or gamma-ray source – a so-called pulsar.









I’m reading right now.
Magnetism~ be the right direction of focused attention. Magnetism is an energy. The unlimited energy precipitating out of the eternally infinite potential; emotions~source of all action in potential.a literally intelligent, emotional, Living Awareness~medium, infinite in volume, infinite in dimensions, infinite in potential.
A new mind set you need. We now look from outside of imperial Creation~ in eternally infinite potential~looking back into the inferior dimensional Creation {with the mind perspective awareness of the superior dimentionalistic potential of i~ infinity √-1=√0-1 as in – √2i=√020-1
E me [email protected] maybe we can quicken each other.
? Nothing of that made any sense, and the terminology looks ripped from science and superstition mixed together.
Think of numerical strings as channels in the medium~Time, and unfolding in an infinite natutre on out thru the greater expanse medium~ i =infinity-1.
One must position themselves upon/in one of these channels, specifically, in space of i~pPotential- thus ط=0~of the potential of i .
So: we go √ 0{=somewheres in i~pPotential}{channel having 2value at channel’s gate in i~pPotential}{in 0=somewheres in i~pPotential}{channel’s gate in i~pPotential}.
Like I said~ A whole new mindset view!
Yershua K
E me.