A newly published study demonstrates how complex cognitive abilities can be incorporated into electronic systems made with neuromorphic chips.
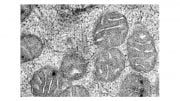
Novel microchips imitate the brain’s information processing in real time. Neuroinformatics researchers from the University of Zurich and ETH Zurich together with colleagues from the EU and US demonstrate how complex cognitive abilities can be incorporated into electronic systems made with so-called neuromorphic chips: They show how to assemble and configure these electronic systems to function in a way similar to an actual brain.
No computer works as efficiently as the human brain – so much so that building an artificial brain is the goal of many scientists. Neuroinformatics researchers from the University of Zurich and ETH Zurich have now made a breakthrough in this direction by understanding how to configure so-called neuromorphic chips to imitate the brain’s information processing abilities in real-time. They demonstrated this by building an artificial sensory processing system that exhibits cognitive abilities.
New approach: simulating biological neurons
Most approaches in neuroinformatics are limited to the development of neural network models on conventional computers or aim to simulate complex nerve networks on supercomputers. Few pursue the Zurich researchers’ approach to develop electronic circuits that are comparable to a real brain in terms of size, speed, and energy consumption. “Our goal is to emulate the properties of biological neurons and synapses directly on microchips,” explains Giacomo Indiveri, a professor at the Institute of Neuroinformatics (INI), of the University of Zurich and ETH Zurich.
The major challenge was to configure networks made of artificial, i.e. neuromorphic, neurons in such a way that they can perform particular tasks, which the researchers have now succeeded in doing: They developed a neuromorphic system that can carry out complex sensorimotor tasks in real time. They demonstrate a task that requires a short-term memory and context-dependent decision-making – typical traits that are necessary for cognitive tests. In doing so, the INI team combined neuromorphic neurons into networks that implemented neural processing modules equivalent to so-called “finite-state machines” – a mathematical concept to describe logical processes or computer programs. Behavior can be formulated as a “finite-state machine” and thus transferred to the neuromorphic hardware in an automated manner. “The network connectivity patterns closely resemble structures that are also found in mammalian brains,” says Indiveri.
Chips can be configured for any behavior modes
The scientists thus demonstrate for the first time how a real-time hardware neural-processing system where the user dictates the behavior can be constructed. “Thanks to our method, neuromorphic chips can be configured for a large class of behavior modes. Our results are pivotal for the development of new brain-inspired technologies,” Indiveri sums up. One application, for instance, might be to combine the chips with sensory neuromorphic components, such as an artificial cochlea or retina, to create complex cognitive systems that interact with their surroundings in real time.
Reference: “Synthesizing cognition in neuromorphic electronic systems” by Emre Neftci, Jonathan Binas, Ueli Rutishauser, Elisabetta Chicca, Giacomo Indiveri and Rodney J. Douglas, 22 July 2013, Proceedings of the National Academy of Sciences.
DOI: 10.1073/pnas.1212083110
Never miss a breakthrough: Join the SciTechDaily newsletter.
Follow us on Google and Google News.
1 Comment
I’ve adapted this in my Sci-Fi thrillers”ORION”S BELT”. But I’ve taken it even farther into the realm of the unknown. I had the Scientists’ that create it, make it both intertwine in a miniature Nano state, combining robotic & biologic nano construction .In the 1st book “ORION’S BELT”Birth of the Hunter, I try to explain it in more synaptic detail. I wrote the manuscript & finished it in April of 2011. This is definitely the wave of the future, and I’m the first Science Fiction author to placate it.