Scientists at Harvard have developed the first model of solid tumor growth that reflects both shape and growth.
They’re among the most powerful tools for demonstrating how cancer grows and spreads, but mathematical models of the disease have always faced an either/or problem.
Models for capturing the spatial — or 3D — aspects of tumors don’t reflect the speed at which they grow. Non-spatial models, meanwhile, can more accurately portray the growth of tumors, but not their 3D nature.
Harvard scientists recently took on the challenge of uniting the two.
A team led by Martin Nowak, director of the Program for Evolutionary Dynamics and a professor of mathematics and of biology, has developed the first model of solid tumor growth that reflects both shape and growth. The study is described in an August 26 paper in the journal Nature.
“Previously, we and many other people used non-spatial models,” Nowak said. “But those models couldn’t possibly explain how a solid tumor could arise. Now, for the first time, we have a spatial model that can do that.”
The key to the new model, Nowak said, is the ability for cells to migrate locally.
“That is what makes cancers grow fast, and it’s what makes cancers homogenous in the sense that cancer cells share a common set of mutations, and what is responsible for the rapid evolution of drug resistance,” Nowak said. “I further believe that the ability to form metastases, which is what actually kills patients, is a consequence of the selection for local migration.”
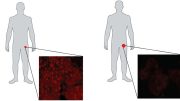
Nowak and colleagues set out to develop better models because the old ones failed to answer critical questions about the proximity of different cells to one another.
“The majority of the mathematical models in the past started with a population of cells, and they would simply count the number of mutations they had,” Nowak said. “But that’s ignoring the spatial structure, so it doesn’t ask which cell is close to another cell.”
Understanding that structure is important, he said, because of the role it plays in how tumors grow.
Earlier spatial models, building on the notion that tumor cells would divide only if they had the necessary space, resulted in slower growth, because only the cells on the surface of the tumor were able to divide.
By giving cells the ability to migrate locally, Nowak said, “individual cells can always find new space where they can divide.”
The result wasn’t just a model that shows faster growth, but one that helps explain why cancer cells share an unusually high number of genetic mutations, and how drug resistance can rapidly evolve in tumors.
All cells — both healthy and cancerous — accumulate mutations as they divide, with most being so-called passenger mutations that have little effect on the cell.
In cancer cells, however, approximately 5 percent are what scientists call “driver” mutations — changes that allow cells to divide faster, live longer, or resist certain drugs. In addition to causing rapid tumor growth, the driver mutations carry all the previous passenger mutations forward. As a result, cancer cells often have a surprising number of mutations in common.
Similarly, drug resistance emerges when cells mutate to become resistant to a particular treatment. While targeted therapies wipe out nearly all other cells, the few resistant cells begin to quickly replicate, causing the patient to relapse.
“This migration ability helps to explain how driver mutations are able to dominate a tumor, and also explains why targeted therapies fail within a few months as resistance evolves,” Nowak said. “So what we have is a mathematical model for solid tumors, and it’s this local migration that explains these questions.”
Reference: “A spatial model predicts that dispersal and cell turnover limit intratumour heterogeneity” by Bartlomiej Waclaw, Ivana Bozic, Meredith E. Pittman, Ralph H. Hruban, Bert Vogelstein and Martin A. Nowak, 26 August 2015, Nature.
DOI: 10.1038/nature14971
Never miss a breakthrough: Join the SciTechDaily newsletter.
Follow us on Google and Google News.