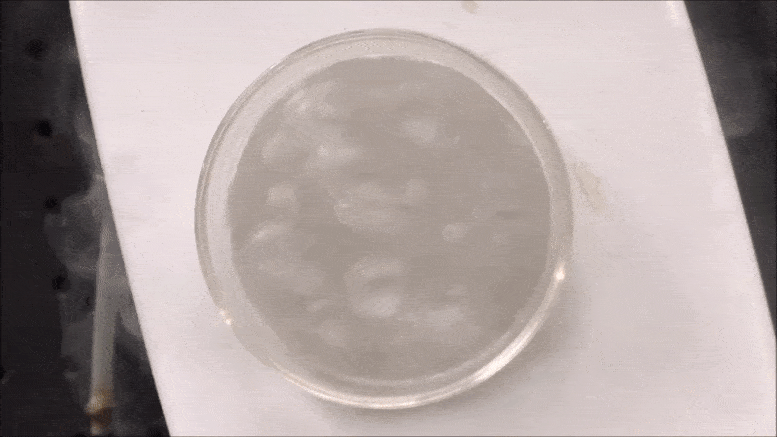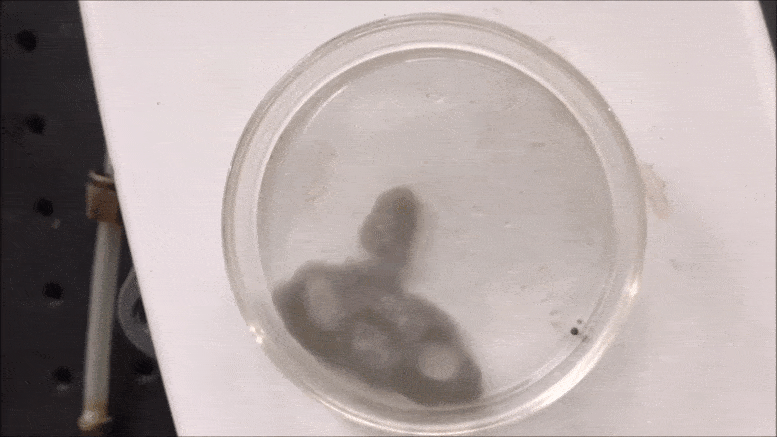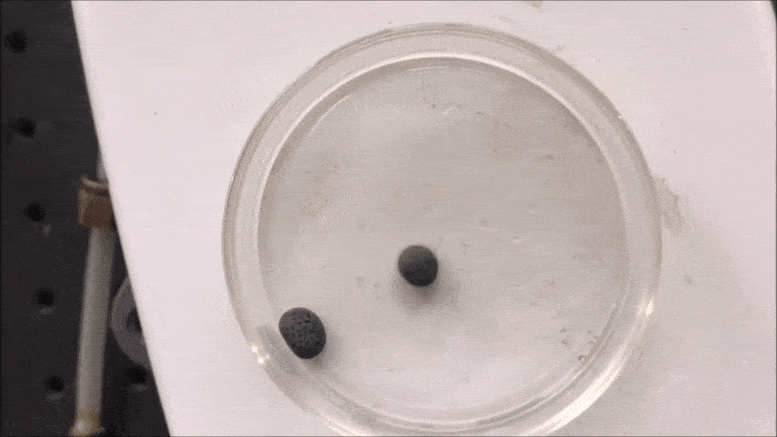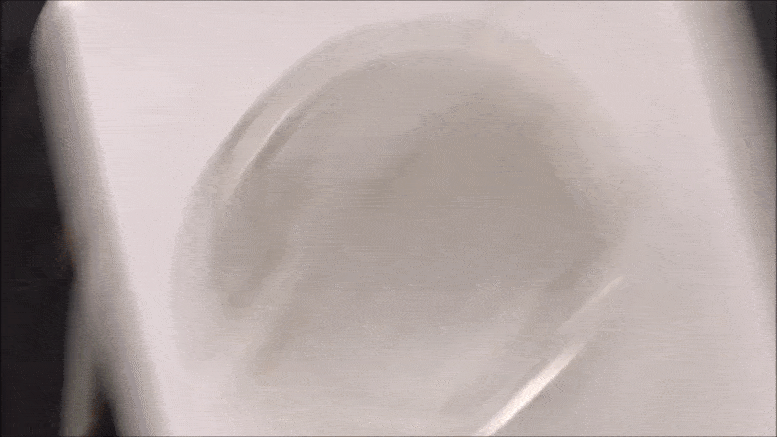
Researchers Create and Stabilize Pure Polymeric Nitrogen Using Plasma for the First Time

Researchers at Drexel University’s C&J Nyheim Plasma Institute have reported that liquid plasma can be used to produce an energy-dense material called polymeric nitrogen. Credit: Drexel University

Producing polymeric nitrogen at near-ambient conditions is a new trick for liquid plasma.

Scientists have long theorized that the energy stored in the atomic bonds of nitrogen could one day be a source of clean energy. But coaxing the nitrogen atoms into linking up has been a daunting task. Researchers at Drexel University’s C&J Nyheim Plasma Institute have finally proven that it’s experimentally possible — with some encouragement from a liquid plasma spark.

Reported in the Journal of Physics D: Applied Physics, the production of pure polymeric nitrogen — polynitrogen — is possible by zapping a compound called sodium azide with a jet of plasma in the middle of a super-cooling cloud of liquid nitrogen. The result is six nitrogen atoms bonded together — a compound called ionic, or neutral, nitrogen-six — that is predicted to be an extremely energy-dense material.

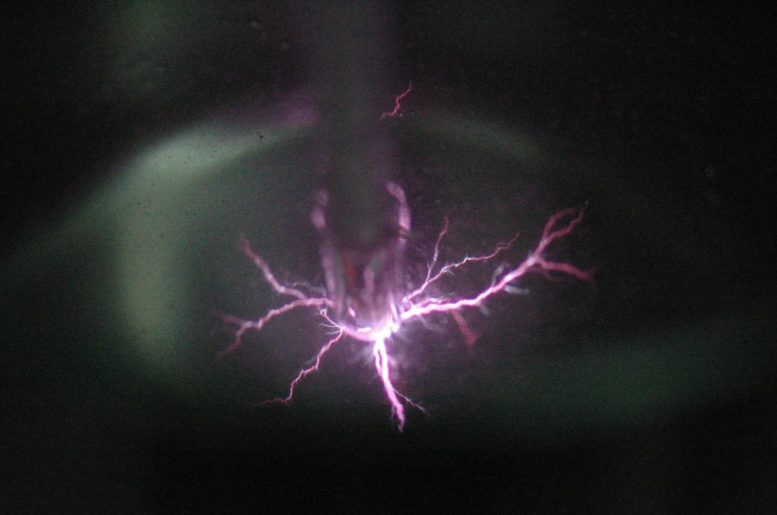
Using a concentrated beam of ions to excite nitrogen compounds in liquid nitrogen, researchers at Drexel’s C&J Nyheim Plasma Institute, have produced an energy-dense material, called polymeric nitrogen, in pure form at near-ambient conditions for the first time. Credit: Drexel University

“Polynitrogen is being explored for use as a ‘green’ fuel source, for energy storage, or as an explosive,” said Danil Dobrynin, Ph.D., an associated research professor at the Nyheim Institute and lead author of the paper. “Versions of it have been experimentally synthesized — though never in a way that was stable enough to recover to ambient conditions or in pure nitrogen-six form. Our discovery using liquid plasma opens a new avenue for this research that could lead to a stable polynitrogen.”

Previous attempts to generate the energetic polymer have used high pressure and high temperature to entice bonding of nitrogen atoms. But neither of those methods provided enough energy to excite the requisite ions — atomic bonding agents — to produce a stable form of nitrogen-six. And the polymeric nitrogen created in these experiments could not be maintained at a pressure and temperature close to normal, ambient conditions.

Researchers at Drexel University’s C&J Nyheim Plasma Institute have reported that liquid plasma can be used to produce an energy-dense material called polymeric nitrogen. Credit: Drexel University

It’s something like trying to glue together two heavy objects but only being strong enough to squeeze a few drops of glue out of the bottle. To make a bond strong enough to hold up, it takes a force strong enough to squeeze out a lot of glue.

That force, according to the researchers, is a concentrated ion blast provided by liquid plasma.

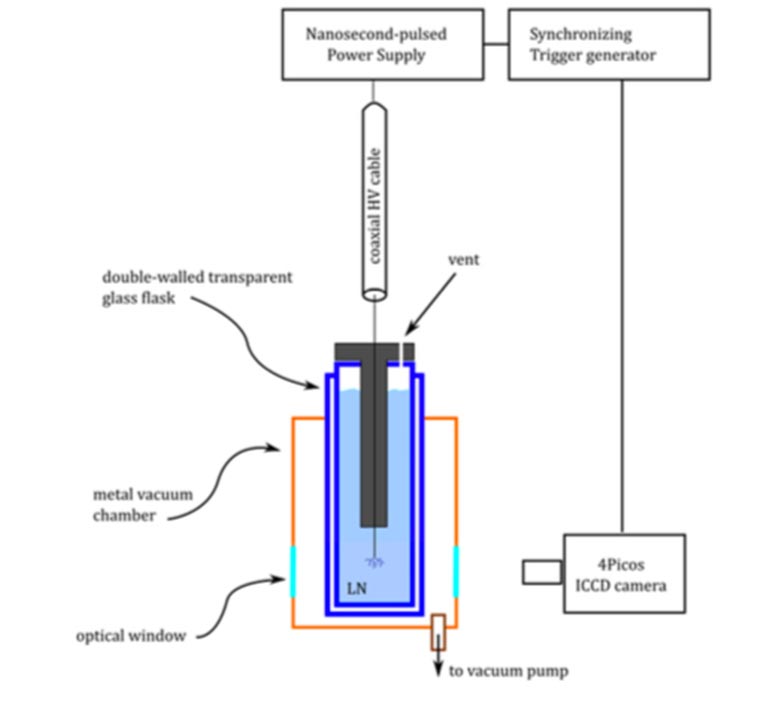
Liquid plasma is the name given to an emission of an ion-dense matter generated by a pulsed electrical spark discharged in a liquid environment — kind of like lightning in a bottle. Liquid plasma technology has barely been around for a decade though it already holds a great deal of promise. It was pioneered by researchers at the Nyheim Institute who have explored is use in a variety of applications, from health care to food treatment.

Because the plasma is encased in liquid it is possible to pressurize the environment, as well as control its temperature. This level of control is the key advantage that the researchers needed to synthesize polynitrogen because it allowed them to more precisely start and stop the reaction in order to preserve the material it produced. Dobrynin and his collaborators first reported their successful attempt to produce polynitrogen using plasma discharges in liquid nitrogen in a letter in the Journal of Physics D: Applied Physics over the summer.

In their most recent findings, the plasma spark sent a concentrated shower of ions toward the sodium azide — which contains nitrogen-three molecules. The blast of ions splits the nitrogen-three molecules from the sodium and, in the excited state, the nitrogen molecules can bond with each other. Not surprisingly, the reaction produces a good bit of heat, so putting the brakes on it requires an incredible blast of cold — the one provided by liquid nitrogen.

“We believe this procedure was successful at producing pure polynitrogen where others fell short, because of the density of ions involved and the presence of liquid nitrogen as a quenching agent for the reaction,” Dobrynin said. “Other experiments introduced high temperatures and high pressures as catalysts, but our experiment was a more precise combination of energy, temperature, electrons, and ions.”

Upon inspection with a Raman spectrometer — an instrument that identifies the chemical composition of a material by measuring its response to laser stimulus — the plasma-treated material produced readings consistent with those predicted for pure polynitrogen.

“This is quite significant because until now scientists have only been able to synthesize stable polynitrogen compounds in the form of salts — but never in a pure nitrogen form like this at near-ambient conditions,” Dobrynin said. “The substance we produced is stable at atmospheric pressure in temperatures up to about -50 Celsius.”

Plasma, in its original gas-laden environment, has been under development for decades as a sterilization technology for water, food, and medical equipment and it is also being explored for coating materials. But this is the first instance of liquid plasma being used to synthesize a new material. So, this breakthrough could prove to be an inflection point in plasma research, at the Nyheim Institute, and throughout the field.

“This discovery opens a number of exciting possibilities for producing polymeric nitrogen as a fuel source,” said Alexander Fridman, Ph.D., John A. Nyheim Chair professor in Drexel’s College of Engineering and director of the C&J Nyheim Plasma Institute and co-author of the paper. “This new, clean energy-dense fuel could enable a new age of automobiles and mass transportation. It could even be the breakthrough necessary to allow the exploration of remote regions of space.”

References:

“Nanosecond-pulsed spark discharge plasma in liquid nitrogen: synthesis of polynitrogen from NaN₃” by Danil Dobrynin, Roman Rakhmanov and Alexander Fridman, 22 August 2019, Journal of Physics D: Applied Physics.
DOI: 10.1088/1361-6463/ab349a

“Nanosecond-pulsed discharge in liquid nitrogen: optical characterization and production of an energetic non-molecular form of nitrogen-rich material” by Danil Dobrynin, Roman Rakhmanov and Alexander Fridman, 22 July 2019, Journal of Physics D: Applied Physics.
DOI: 10.1088/1361-6463/ab30f1

This research was supported by the Army Research Office. In addition to Dobrynin, and Fridman, Roman Rakhmanov of the C&J Nyheim Plasma Institute contributed to this research.