
Mathematicians at Paderborn University and KU Leuven, using the Noctua supercomputer and specialized hardware accelerators, have solved a decades-old problem by calculating the ninth Dedekind number, a mathematical sequence of enormous complexity. The exact number, previously thought uncomputable due to its size, is 286386577668298411128469151667598498812366.
Scientists from the Universities of Paderborn and Leuven solve long-known problem in mathematics.
Making history with 42 digits: Scientists at Paderborn University and KU Leuven have unlocked a decades-old mystery of mathematics with the so-called ninth Dedekind number. Experts worldwide have been searching for the value since 1991. The Paderborn scientists arrived at the exact sequence of numbers with the help of the Noctua supercomputer located there. The results will be presented in September at the International Workshop on Boolean Functions and their Applications (BFA) in Norway.
What started as a master’s thesis project by Lennart Van Hirtum, then a computer science student at KU Leuven and now a research associate at the University of Paderborn, has become a huge success. The scientists join an illustrious group with their work: Earlier numbers in the series were found by mathematician Richard Dedekind himself when he defined the problem in 1897, and later by greats of early computer science such as Randolph Church and Morgan Ward. “For 32 years, the calculation of D(9) was an open challenge, and it was questionable whether it would ever be possible to calculate this number at all,” Van Hirtum says.

Credit: Paderborn University, Besim Mazhiqi
The previous number in the Dedekind sequence, the 8th Dedekind number, was found in 1991 using a Cray 2, the most powerful supercomputer at the time. “It, therefore, seemed conceivable to us that it should be possible by now to calculate the 9th number on a large supercomputer,” says Van Hirtum, describing the motivation for the ambitious project, which he initially implemented jointly with the supervisors of his master’s thesis at KU Leuven.
Grains of sand, chess and supercomputers
The main subject of Dedekind numbers are so-called monotone Boolean functions. Van Hirtum explains, “Basically, you can think of a monotone Boolean function in two, three, and infinite dimensions as a game with an n-dimensional cube. You balance the cube on one corner and then color each of the remaining corners either white or red. There is only one rule: you must never place a white corner above a red one. This creates a kind of vertical red-white intersection. The object of the game is to count how many different cuts there are. Their number is what is defined as the Dedekind number. Even if it doesn’t seem like it, the numbers quickly become gigantic in the process: the 8th Dedekind number already has 23 digits.”
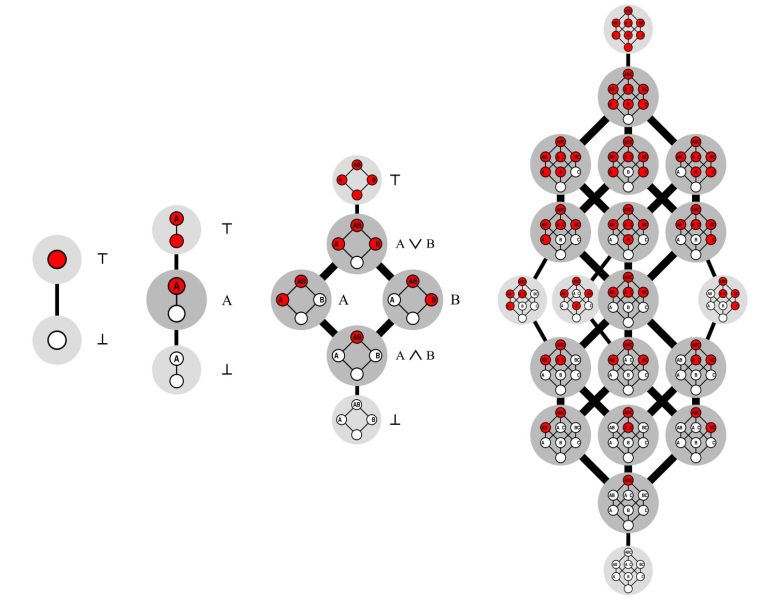
he figure shows all possible cuts for dimensions 0, 1, 2, and 3. The number of these colored 2D, 3D, – N-dimensional cuts that can be formed is what is defined as the Dedekind number. Credit: Paderborn University
Comparably large — but incomparably easier to calculate — numbers are known from a legend concerning the invention of the game of chess. “According to this legend, the inventor of the chess game asked the king for only a few grains of rice on each square of the chess board as a reward: one grain on the first square, two grains on the second, four on the third, and twice as many on each of the following squares. The king quickly realized that this request was impossible to fulfill, because so much rice does not exist in the whole world. The number of grains of rice on the complete board would have 20 digits — an unimaginable amount, but still less than D(8). When you realize these orders of magnitude, it is obvious that both an efficient computational method and a very fast computer would be needed to find D(9),” Van Hirtum said.
Milestone: Years become months
To calculate D(9), the scientists used a technique developed by master’s thesis advisor Patrick De Causmaecker known as the P-coefficient formula. It provides a way to calculate Dedekind numbers not by counting, but by a very large sum. This allows D(8) to be decoded in just eight minutes on a normal laptop. But, “What takes eight minutes for D(8) becomes hundreds of thousands of years for D(9). Even if you used a large supercomputer exclusively for this task, it would still take many years to complete the calculation,” Van Hirtum points out. The main problem is that the number of terms in this formula grows incredibly fast. “In our case, by exploiting symmetries in the formula, we were able to reduce the number of terms to ‘only’ 5.5*10^18 — an enormous amount. By comparison, the number of grains of sand on Earth is about 7.5*10^18, which is nothing to sneeze at, but for a modern supercomputer, 5.5*10^18 operations are quite manageable,” the computer scientist said. The problem: The calculation of these terms on normal processors is slow and also a use of GPUs as currently the fastest hardware accelerator technology for many AI applications is not efficient for this algorithm.
The solution: application-specific hardware using highly specialized and parallel arithmetic units — so-called FPGAs (field programmable gate arrays). Van Hirtum developed an initial prototype for the hardware accelerator and began looking for a supercomputer that had the necessary FPGA cards. In the process, he became aware of the Noctua 2 computer at the “Paderborn Center for Parallel Computing (PC2)” at the University of Paderborn, which has one of the world’s most powerful FPGA systems.
Prof. Dr. Christian Plessl, head of PC2, explains: “When Lennart Van Hirtum and Patrick De Causmaeker contacted us, it was immediately clear to us that we wanted to support this moonshot project. Solving hard combinatorial problems with FPGAs is a promising field of application and Noctua 2 is one of the few supercomputers worldwide with which the experiment is feasible at all. The extreme reliability and stability requirements also pose a challenge and test for our infrastructure. The FPGA expert consulting team worked closely with Lennart to adapt and optimize the application for our environment.”
After several years of development, the program ran on the supercomputer for about five months. And then the time had come: on March 8, the scientists found the 9th Dedekind number: 286386577668298411128469151667598498812366.
Today, three years after the start of the Dedekind project, Van Hirtum is working as a fellow of the NHR Graduate School at the Paderborn Center for Parallel Computing to develop the next generation of hardware tools in his PhD. The NHR (National High Performance Computing) Graduate School is the joint graduate school of the NHR centers. He will report on his extraordinary success together with Patrick De Causmaecker on June 27 at 2 p.m. in Lecture Hall O2 of the University of Paderborn. The interested public is cordially invited.








As a mechanical engineer, I deal with numbers and math formulas on a regular basis… but every time I read about these extremely complex mathematical problems that scientists spend their entire lives trying to solve, I can’t help but feel like my tiny, dumb midget brain just got put through a shredder and then painstakingly reassembled by those very same scientists. Truly amazing the things they do.
You have a magnificent brain my dear, don’t sell yourself short for your chosen methodology. They’ve had other reasons, other ventures, other influences. You are amazing, never forget that! <3
Interesting, amazing, and useless? Why should one not think this was an interesting and useless waste of human and natural resources?
I can’t say for certain what their purpose is, but I would assume that they are calculating the functional movement of 4th dimensional matter. It’s awfully close to a Metatron Cube.
Being able to capture 4th dimensional matter would be the first step to utilizing 4th dimensional motor function in three-dimensional open space. I’d say this is an outstanding next step for our species. 🙂
The same was most likely said once about Calculus, Group Theory and Number Theory.
A lot of things which seem useless turn out to have incredible applications later on.
If one were to align atoms in this particular function, they would naturally, albeit eventually; curve around one another, stretching through the wall of polarized matter, wouldn’t they theoretically create a fourth dimensional magnet?
This is proof that maths is wicked!