
The two computer scientists, Assistant Professor Jacob Holm of UCPH and Associate Professor Eva Rotenberg of DTU almost gave their solution away in the summer of 2019, after submitting a research article that became the precursor to the article in which they finally solved the math riddle. Credit: University of Copenhagen
Researchers thought that they were five years away from solving a math riddle from the 1980s. In reality, and without knowing, they had nearly cracked the problem already.
Researchers from the University of Copenhagen and the Technical University of Denmark (DTU) thought that they were five years away from solving a math riddle from the 1980s. In reality, and without knowing, they had nearly cracked the problem and had just given away much of the solution in a research article. The solution could be used to improve tomorrow’s phones and computers.
A veritable brain teaser. That’s how one can safely describe this mathematical problem in the discipline of graph theory. Two mathematicians from the University of Copenhagen’s Department of Computer Science and DTU have now solved a problem that the world’s quickest and most clever have been struggling with since the 1980s.
The two computer scientists, Assistant Professor Jacob Holm of UCPH and Associate Professor Eva Rotenberg of DTU almost gave their solution away in the summer of 2019, after submitting a research article that became the precursor to the article in which they finally solved the math riddle.
“We had nearly given up on getting the last piece and solving the riddle. We thought we had a minor result, one that was interesting, but in no way solved the problem. We guessed that there would be another five years of work, at best, before we would be able to solve the puzzle,” explains Jacob Holm, who is a part of BARC, the algorithm section at UCPH’s Department of Computer Science.
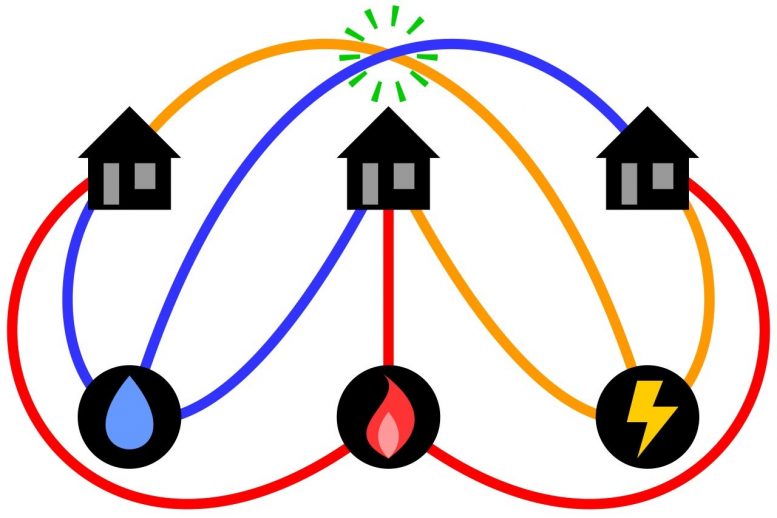
In 1913, a precursor to the now-solved mathematical conundrum was published in “The Strand Magazine” as “The Three Utilities Problem”. It caused the magazine’s readers to scratch their heads and ponder. In the problem, each of the three cottages must have water, gas, and electricity, while the “lines” between the houses and water, electricity, and gas may not cross each other — which is not possible. Credit: University of Copenhagen
A solution between the lines
Simply put, the puzzle is about how to connect a number of points in a graph without allowing the lines connecting them to cross. And how with a mathematical calculation — an algorithm — you can make changes to an extensive “graph network” to ensure that no lines intersect without having to start all over again. Properties that can be used for, among other things, building immense road networks or the tiny innards of computers, where electrical circuitry on circuit boards may not cross.
Jacob Holm has been interested in the mathematical conundrum since 1998, but the answer was only revealed while the two researchers were reading through their already submitted research article. In the meantime, the researchers heard about a novel mathematical technique that they realized could be applied to the problem.
“While reading our research article, we suddenly realized that the solution was before our eyes. Our next reaction was ‘oh no – we’ve shot ourselves in the foot and given away the solution,’ says Associate Professor Eva Rotenberg of DTU.
Could be used for computer electronics
This is when the two researchers got busy writing the research paper and tying up loose ends to solve the conundrum that Holm had been working on intermittently since 1998.
“We worked on the article non-stop, for five to six weeks. And, it ended up filling more than 80 pages,” says Eva Rotenberg.
Fortunately, no one beat them to the solution and the two researchers were able to present their results at the main theoretical computer science conferences, which were meant to be held in Chicago, but ended up being held virtually.
So, what can the solution to this mathematical conundrum be used for? The two researchers don’t know for sure, but they have a few suggestions.
“Our research is basic research, so we rarely know what it will end up being used for. Even from the start, we find applications difficult to imagine,” says Jacob Holm, who adds:
“The design of microchips and circuit boards, found in all electronics, could be an area where our result ends up being used. When drawing wires on a circuit board, they must never intersect. Otherwise, short circuits will occur. The same applies to microchips, which contain millions of transistors and for which one must have a graph drawing.”
About graph theory
A GRAPH is a very simple construction used to model things that can be described as objects and the connections between them. Graph theory is both an area of mathematics and an important tool in computer science.
In this context, a graph can be illustrated by a diagram consisting of a number of points (nodes, vertices) associated with a number of lines (edges). Each edge is illustrated as a line (or curved piece) with nodes as its two endpoints.
About the solution
There are two kinds of updates in dynamic graphs: One can delete an edge and one can insert a new edge. These two operations must be made by the user, while an algorithm keeps track of the network’s drawing at all times. This is the algorithm that the researchers have found the recipe for.
Reference: “Fully-dynamic Planarity Testing in Polylogarithmic Time” by Jacob Holm and Eva Rotenberg, 10 December 2019, Computer Science > Data Structures and Algorithms.
arXiv: 1911.03449







There is a trivial solution to that 3×3 problem: leave 2 dimensions behind and consider 3 dimensions instead.
“Fully-dynamic Planarity Testing in Polylogarithmic Time”
The issue lies in testing for planar embeddings of graphs, so jumping into the 3rd dimension isn’t an option.
Reminds me of learning PCB design… I learned to make those untangled connections because every via and drill holes cost real money!
What a s#!t article. Did you understand what you were writing about?
Yes, I did. But maybe because graph theory is really foundational in many fields today.
Why does this array have to be in the layout as shown? Is that part of this puzzle? Moving “Water” to above house 1 would eliminate all crossings if the illustration is changeable. I’m expert at threads, yarn, strings, loops, and some knots, as well as tessellation, repeat designs and layout. Despite all this, I find this topic fascinating.
The array layout is for simplicity. But as you can imagine, rotating or else distorting the layout makes the same graph problem (or else what use would a graph have).
Making that move will not eliminate all crossings. It will eliminate the current crossing, but create a new one – likely water to house 2 and electricity to house 1. Feel free to try drawing it yourself (I have also spent many hours fiddling with situations that have already been proved impossible), but this fact – that a K(3,3) graph is not planar – is an elementary graph theory proof.
No. Move water to above house 1 won’t eliminate all crossing. In this case, while the original water line won’t cross the middle power line, it would cause another water line cross the power line.
Kobayashi Maru.
😸
To those not bothering to read everything, the house riddle is an unsolvable riddle from 1913 — see the caption — it was just the inspiration for the 1980s puzzle. The article is not about the houses.
Morgan, moving water to there is topologically identical to leaving it where it is
I’ve always wonder where that S everyone in middle school use to draw came from. Tesla solved the 3 utilities puzzle before everybody (wireless transmission of electricity) lol but in all seriousness I’d like to see the formula expression
Can’t you just use a circular pattern? I drew it out easily and never once cried a line.
No, you want the direct connection by definition of the graph. (Also, in most real cases you have mains for robustness and what not.)
Can’t you just use a circular pattern? I drew it out easily and never once crossed a line.
So… So you have a picture of the solution?
No, but they have a software that will tell you there is no such picture.
Solve it in 3D.
As the article describes, that is generally unfeasible for electronics (say).
If the constraint is that the 3 houses and 3 utilities must be located on a plane, then let’s use a real projective plane, in other words, a Moebius strip. We are not using three dimensions to cheat. A Moebius strip has just one side, one edge and no thickness. It definitely does not have three dimensions and is a plane of a special type. After drawing all the utility lines but two, we send the last two lines away from the houses out along the surface, making sure that the houses and lines “bleed through” the paper we are using to represent the Moebius strip. (OK, that part may be cheating mathematically speaking, but it makes for a cool way to win a bet, maybe.) After all, if the plane has a thickness of zero (we argue), you can see the houses and lines from the other side of our paper Moebius strip. Use a thick marker when drawing this puzzle! When the two lines reappear on the far side of the houses, they are reversed without having crossed each other and connect easily to the houses.
When VLSI electronics moves to plastic, they may adopt that (or not, since it takes up lots of space, warp the substrate, et cetera).
I agree with others. Adding “time” to 2D is adding a third dimension. Turning on and off a line regardless it’s dynamic location is a form of another dimension. Hence the solution could involve more if any dimension spacial or time could be introduced.
Sure, but that is no longer a planar graph for the problems that it would solve.
If you run the same line to all three houses then the other two supply’s can be dispersed to all without crossing
You folks have too much education, run the lines parallel through the houses and I solved that puzzle the first time I saw it when it was published LOL
HEY! Wheres the cable! LOL
Mmm back. In time
I started attempting to solve this since 1967 when my fifth grade teacher brought presented to our class.
What about using a “Mobius strip” approach, unless you are working in only a single dimension. Then the application does not apply to real science/life, and you can make up any rule you want.
Hey sorry, I did not read the whole comment section, missed the guys comment on the 17th. But it just seemed to be the obvious approach.
I didn’t know if I would smile or frown when I got through the article and then the comments and see someone – like most of the comments – not seeming to have read the article (or want to pull each other’s legs) but commenting on not having read the comments section discussing irrelevancies.
Oy!
Do they have any rights for the solution or does it all belong to the university?
… I guess they didn’t use quantum computers to solve that, then there would be a solution for that too…
My solution might be equivalent to others mentioned here, but it seems to me you could solve the problem by putting the electrical source IN the center house.