Physicists Explore Unknown Energy Regions – “New Frontier of Physics”

Florida State graduate student Jason Barlow works on a part of the GlueX detector at Jefferson National Laboratory. FSU scientists painted the part of the GlueX detector they built garnet and gold. Credit: FSU

Photon-proton collisions are being used by physicists at Florida State University to capture particles in an undiscovered energy range, revealing fresh insights into the substance that holds the nucleus together.

“We want to understand not just the nucleus, but everything that makes up the nucleus,” said FSU Professor of Physics Paul Eugenio. “We’re working to understand the particles and forces that make up our world.”

FSU’s hadronic physics group is a leading member of the GlueX Collaboration at the U.S. Department of Energy’s Thomas Jefferson National Accelerator Facility. The group ran highly sophisticated experiments around the clock for months at a time over several years starting in 2016. Their primary objective is to discover new knowledge on the substance, known as the gluonic field, that binds quarks together. Quarks are the basic particles from which protons and neutrons are created.

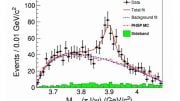
In a new paper published in Physical Review Letters, the hadronic physics group at Florida State University and their collaborators laid out the first-ever measurements of a subatomic particle — called the J/psi particle —  created out of the energy in the photon-proton collisions.

“It’s really cool to see,” said Assistant Professor of Physics Sean Dobbs. “This is opening up a new frontier of physics.”

When researchers run these experiments, they blast a photon beam into the GlueX spectrometer where it passes through a canister of liquid hydrogen and reacts with the protons in the nucleus of these hydrogen atoms. From there, the detectors measure the particles created in these collisions, which allows physicists to reconstruct the details of the collision and learn more about the created particles.

Dobbs compared it to a car wreck. You might not see the wreck happen, but you see the result and can work backward. In this case, researchers collected about one to two million gigabytes of data per year through this process to try to piece together the puzzle.

The J/psi particle is composed of a pair of quarks – a charm quark and an anti-charm quark. In measuring the J/psi particle in these collisions, scientists can also look for the production of other charm quark-containing subatomic particles.

The measurements were taken at an energy threshold below where previous studies looked at production levels, meaning it was more sensitive to the distribution of the gluons in the proton and their contributions to the proton mass.

Scientists found a much larger production of J/psi particles than expected, meaning this gluonic structure is a big contributor to the mass of the proton structure, and thus the nucleus as a whole. These initial measurements suggest that the gluons directly contribute more than 80 percent of the mass of the proton. Further measurements of these reactions currently underway will give more insight into how the gluons are distributed around the nucleon.

These measurements also brought into question observations from experiments on the Large Hadron Collider, a particle detector at CERN, the European Organization for Nuclear Research. Scientists there briefly glimpsed what they are calling pentaquarks – short-lived particles made of five quarks.

FSU physicists did not specifically see pentaquarks in their data, which has ruled out several models that attempt to describe the structure of these pentaquarks. Further measurements underway are expected to give a more definitive answer on how the five quarks are arranged in these particles.

###

This work is funded by the Department of Energy and supported by the Thomas Jefferson National Accelerator Facility. The GlueX collaboration involves scientists from 29 institutions around the world.

FSU Professor Volker Credé, FSU Scientists Alexander Ostrovidov, postdoctoral fellow Daniel Lersch, and several FSU graduate students contributed to this work. The graduate students are Jason Barlow, Edmundo Barriga, Bradford Cannon, Ashley Ernst, Angelica Goncalves, and Lawrence Ng.

Reference: “First Measurement of Near-Threshold $J/\psi$ Exclusive Photoproduction off the Proton” by A. Ali et al. (GlueX Collaboration), 13 August 2019, Physical Review Letters.
DOI: 10.1103/PhysRevLett.123.072001