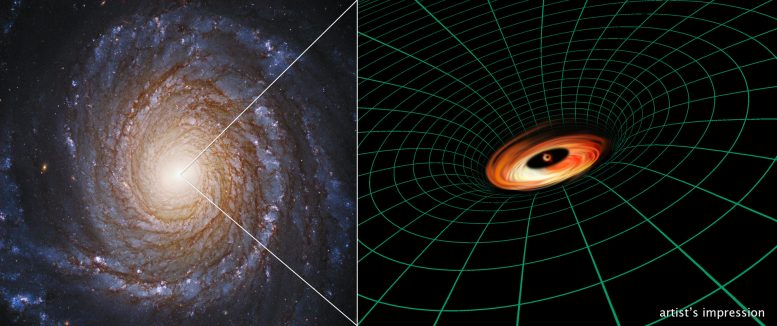
A Hubble Space Telescope image of the spiral galaxy NGC 3147 appears next to an artist’s illustration of the supermassive black hole residing at the galaxy’s core. The Hubble image shows off the galaxy’s sweeping spiral arms, full of young blue stars, pinkish nebulas, and dust in silhouette. However, at the brilliant core of NGC 3147 lurks a monster black hole, weighing about 250 million times the mass of our Sun. Hubble observations of the black hole demonstrate two of Einstein’s theories of relativity. The reddish-yellow features swirling around the center are the glow of light from gas trapped by the hefty black hole’s powerful gravity. The black hole is embedded deep within its gravitational field, shown by the green grid that illustrates warped space. The gravitational field is so strong that light is struggling to climb out, a principal described in Einstein’s theory of general relativity. Material also is whipping so fast around the black hole that it brightens as it approaches Earth on one side of the disk and gets fainter as it moves away. This effect, called relativistic beaming, was predicted by Einstein’s theory of special relativity. NGC 3147 is located 130 million light-years away in the northern circumpolar constellation Draco the Dragon. Credit: Hubble Image: NASA, ESA, S. Bianchi (Università degli Studi Roma Tre University), A. Laor (Technion-Israel Institute of Technology), and M. Chiaberge (ESA, STScI, and JHU); illustration: NASA, ESA, and A. Feild and L. Hustak (STScI)
As if black holes weren’t mysterious enough, astronomers using NASA’s Hubble Space Telescope have found an unexpected thin disk of material furiously whirling around a supermassive black hole at the heart of the magnificent spiral galaxy NGC 3147, located 130 million light-years away.
The conundrum is that the disk shouldn’t be there, based on current astronomical theories. However, the unexpected presence of a disk so close to a black hole offers a unique opportunity to test Albert Einstein’s theories of relativity. General relativity describes gravity as the curvature of space and special relativity describes the relationship between time and space.
“We’ve never seen the effects of both general and special relativity in visible light with this much clarity,” said Marco Chiaberge of the European Space Agency, and the Space Telescope Science Institute and Johns Hopkins University, both in Baltimore, Maryland, a member of the team that conducted the Hubble study.
“This is an intriguing peek at a disk very close to a black hole, so close that the velocities and the intensity of the gravitational pull are affecting how the photons of light look,” added the study’s first author, Stefano Bianchi of Università degli Studi Roma Tre, in Rome, Italy. “We cannot understand the data unless we include the theories of relativity.”
Black holes in certain types of galaxies like NGC 3147 are malnourished because there is not enough gravitationally captured material to feed them regularly. So, the thin haze of infalling material puffs up like a donut rather than flattening out in a pancake-shaped disk. Therefore, it is very puzzling why there is a thin disk encircling a starving black hole in NGC 3147 that mimics much more powerful disks found in extremely active galaxies with engorged, monster black holes.
“We thought this was the best candidate to confirm that below certain luminosities, the accretion disk doesn’t exist anymore,” explained Ari Laor of the Technion-Israel Institute of Technology located in Haifa, Israel. “What we saw was something completely unexpected. We found gas in motion producing features we can explain only as being produced by material rotating in a thin disk very close to the black hole.”
The astronomers initially selected this galaxy to validate accepted models about lower-luminosity active galaxies—those with black holes that are on a meager diet of material. Models predict that an accretion disk forms when ample amounts of gas are trapped by a black hole’s strong gravitational pull. This infalling matter emits lots of light, producing a brilliant beacon called a quasar, in the case of the most well-fed black holes. Once less material is pulled into the disk, it begins to break down, becomes fainter, and changes structure.
“The type of disk we see is a scaled-down quasar that we did not expect to exist,” Bianchi said. “It’s the same type of disk we see in objects that are 1,000 or even 100,000 times more luminous. The predictions of current models for gas dynamics in very faint active galaxies clearly failed.”
The disk is so deeply embedded in the black hole’s intense gravitational field that the light from the gas disk is modified, according to Einstein’s theories of relativity, giving astronomers a unique look at the dynamic processes close to a black hole.
Hubble clocked material whirling around the black hole as moving at more than 10% of the speed of light. At those extreme velocities, the gas appears to brighten as it travels toward Earth on one side and dims as it speeds away from our planet on the other side (an effect called relativistic beaming). Hubble’s observations also show that the gas is so entrenched in the gravitational well that the light is struggling to climb out, and therefore appears stretched to redder wavelengths. The black hole’s mass is around 250 million Suns.
The researchers used Hubble’s Space Telescope Imaging Spectrograph (STIS) to observe matter swirling deep inside the disk. A spectrograph is a diagnostic tool that divides light from an object into its many individual wavelengths to determine its speed, temperature, and other characteristics at a very high precision. The astronomers needed STIS’s sharp resolution to isolate the faint light from the black-hole region and block out contaminating starlight.
“Without Hubble, we wouldn’t have been able to see this because the black-hole region has a low luminosity,” Chiaberge said. “The luminosities of the stars in the galaxy outshine anything in the nucleus. So if you observe it from the ground, you’re dominated by the brightness of the stars, which drowns the feeble emission from the nucleus.”
The team hopes to use Hubble to hunt for other very compact disks around low-wattage black holes in similar active galaxies.
Reference: “HST unveils a compact mildly relativistic broad-line region in the candidate true type 2 NGC 3147” by Stefano Bianchi, Robert Antonucci, Alessandro Capetti, Marco Chiaberge, Ari Laor, Loredana Bassani, Francisco J Carrera, Fabio La Franca, Andrea Marinucci, Giorgio Matt, Riccardo Middei and Francesca Panessa, 11 July 2019, Monthly Notices of the Royal Astronomical Society.
DOI: 10.1093/mnrasl/slz080
The Hubble Space Telescope is a project of international cooperation between NASA and ESA (European Space Agency). NASA’s Goddard Space Flight Center in Greenbelt, Maryland, manages the telescope. The Space Telescope Science Institute (STScI) in Baltimore, Maryland, conducts Hubble science operations. STScI is operated for NASA by the Association of Universities for Research in Astronomy in Washington, D.C.









You can see 130000000 light years away but you can’t find Nibaru.