
Simulation of M87 black hole showing the motion of plasma as it swirls around the black hole. The bright thin ring that can be seen in blue is the edge of what we call the black hole shadow. Credit: L. Medeiros; C. Chan; D. Psaltis; F. Özel; UArizona; IAS.
Einstein’s description of gravity just got much harder to beat after astrophysicists put general relativity to a new test with black hole images.
Einstein’s theory of general relativity — the idea that gravity is matter warping spacetime — has withstood over 100 years of scrutiny and testing, including the newest test from the Event Horizon Telescope collaboration, published today in the latest issue of Physical Review Letters.
According to the findings, Einstein’s theory just got 500 times harder to beat.
Despite its successes, Einstein’s robust theory remains mathematically irreconcilable with quantum mechanics, the scientific understanding of the subatomic world. Testing general relativity is important because the ultimate theory of the universe must encompass both gravity and quantum mechanics.
“We expect a complete theory of gravity to be different from general relativity, but there are many ways one can modify it. We found that whatever the correct theory is, it can’t be significantly different from general relativity when it comes to black holes. We really squeezed down the space of possible modifications,” said UArizona astrophysics professor Dimitrios Psaltis, who until recently was the project scientist of the Event Horizon Telescope collaboration. Psaltis is the lead author of a new paper that details the researchers’ findings.
“This is a brand-new way to test general relativity using supermassive black holes,” said Keiichi Asada, an EHT science council member and an expert on radio observations of black holes for Academia Sinica Institute of Astronomy and Astrophysics.

Visualization of the new gauge developed to test the predictions of modified gravity theories against the measurement of the size of the M87 shadow. Credit: D. Psaltis, UArizona; EHT Collaboration
To perform the test, the team used the first image ever taken of the supermassive black hole at the center of nearby galaxy M87 obtained with the EHT last year. The first results had shown that the size of the black-hole shadow was consistent with the size predicted by general relativity.
“At that time, we were not able to ask the opposite question: How different can a gravity theory be from general relativity and still be consistent with the shadow size?” said UArizona Steward Theory Fellow Pierre Christian. “We wondered if there was anything we could do with these observations in order to cull some of the alternatives.”
The team did a very broad analysis of many modifications to the theory of general relativity to identify the unique characteristic of a theory of gravity that determines the size of a black hole shadow.
“In this way, we can now pinpoint whether some alternative to general relativity is in agreement with the Event Horizon Telescope observations, without worrying about any other details,” said Lia Medeiros, a postdoctoral fellow at the Institute for Advanced Study who has been part of the EHT collaboration since her time as a UArizona graduate student.
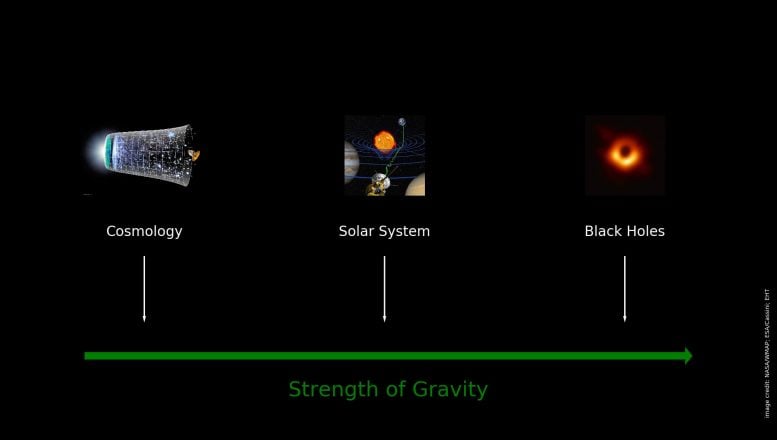
Illustration of the different strengths of gravitational fields probed by cosmological, solar-system, and black-hole tests. Credit: D. Psaltis, UArizona; NASA/WMAP; ESA/Cassini; EHT collaboration
The team focused on the range of alternatives that had passed all the previous tests in the solar system.
“Using the gauge we developed, we showed that the measured size of the black hole shadow in M87 tightens the wiggle room for modifications to Einstein’s theory of general relativity by almost a factor of 500, compared to previous tests in the solar system,” said UArizona astrophysics professor Feryal Özel, a senior member of the EHT collaboration. “Many ways to modify general relativity fail at this new and tighter black hole shadow test.”
“Black hole images provide a completely new angle for testing Einstein’s theory of general relativity,” said Michael Kramer, director of the Max Planck Institute for Radio Astronomy and EHT collaboration member.
“Together with gravitational wave observations, this marks the beginning of a new era in black hole astrophysics,” Psaltis said.
Testing the theory of gravity is an ongoing quest: Are the general relativity predictions for various astrophysical objects good enough for astrophysicists to not worry about any potential differences or modifications to general relativity?
“We always say general relativity passed all tests with flying colors — if I had a dime for every time I heard that,” Özel said. “But it is true, when you do certain tests, you don’t see that the results deviate from what general relativity predicts. What we’re saying is that while all of that is correct, for the first time we have a different gauge by which we can do a test that’s 500 times better, and that gauge is the shadow size of a black hole.”
Next, the EHT team expects higher fidelity images that will be captured by the expanded array of telescopes, which includes the Greenland Telescope, the 12-meter Telescope on Kitt Peak near Tucson, and the Northern Extended Millimeter Array Observatory in France.
“When we obtain an image of the black hole at the center of our own galaxy, then we can constrain deviations from general relativity even further,” Özel said.
Will Einstein still be right, then?
Read Unique Test of General Relativity Using a Black Hole for more on this study.
Reference: “Gravitational Test beyond the First Post-Newtonian Order with the Shadow of the M87 Black Hole” by Dimitrios Psaltis et al. (EHT Collaboration), 1 October 2020, Physical Review Letters.
DOI: 10.1103/PhysRevLett.125.141104
The international collaboration of the Event Horizon Telescope announced the first-ever image of a black hole at the heart of the radio galaxy Messier 87 on April 10, 2019 by creating a virtual Earth-sized telescope. Supported by considerable international investment, the EHT links existing telescopes using novel systems — creating a new instrument with the highest angular resolving power that has yet been achieved.
The individual telescopes involved in the EHT collaboration are: the Atacama Large Millimeter/submillimeter Array (ALMA), the Atacama Pathfinder EXplorer (APEX), the Greenland Telescope (since 2018), the IRAM 30-meter Telescope, the NOEMA Observatory (expected 2021), the Kitt Peak Telescope (expected 2021), the James Clerk Maxwell Telescope (JCMT), the Large Millimeter Telescope (LMT), the Submillimeter Array (SMA), the Submillimeter Telescope (SMT), and the South Pole Telescope (SPT).
The EHT consortium consists of 13 stakeholder institutes; the Academia Sinica Institute of Astronomy and Astrophysics, the University of Arizona, the University of Chicago, the East Asian Observatory, the Harvard-Smithsonian Center for Astrophysics, the Goethe-Universita?t Frankfurt, the Institut de Radioastronomie Millime?trique, the Large Millimeter Telescope, the Max-Planck-Institut fu?r Radioastronomie, the MIT Haystack Observatory, the National Astronomical Observatory of Japan, the Perimeter Institute for Theoretical Physics, and the Radboud University.







The usual argument against Einstein’s general relativity (GR) is that it is not compatible with quantum mechanics (QM). By that it is meant that viewing gravity as a “field” like the electromagnetic field(EM)leads to an infinite set of infinities in the calculations that cannot be transformed into finite quantities. Hence one seeks for an alternative “field” to replace GR that might be “renormalizable.” Perhaps the problem is in QM which is written only in a flat spacetime. But a free electron in QM has a non-zero probability of being ANYWHERE in the universe including non-flat areas of spacetime. Perhaps a QM that not only was generally covariant (consistent with any spacetime) but contributed to the spacetime curvature is what is needed. One theory (GR) is not subsumed by the other (QM), but both merge together.
Good points! I’m sorry for the lengthy response, but I was just thinking this over and it is easier to make a verbose response than trying to condense it furher.
My own analysis is influenced by recent cosmology, where space is on average flat over sufficiently large volumes. And I find it encouraging that by simply making a quantum field theory of the linearized Einstein equations that fit one gets a theory that works on flat spacetime and works well [ http://www.scholarpedia.org/article/Quantum_gravity_as_a_low_energy_effective_field_theory ]. We now know that cosmology inhabits the low-field limit (see that figure), since inflation has an exponentially decreasing scale factor on flat space (and singularity theorems claiming a singularity would happen have problems).
The only case where you get close to strong-field effects is black holes (see that figure again). And there are models – however daft – of black holes that avoid Planck scale singularities, such as dark energy + curved space “GEODEs”. It seems to be easy to show with collapsing dust models that a spherical collapse as forced by gravity doesn’t need to be an inherent problem for such smoother solutions [more than one link would put the comment in a queue for moderation, so I appeal to web searches from here on].
And if you always stay well below Planck scale in the universe, the low energy quantum field theory should describe the physics without having to handle an infinite number of parameters in a renormalization realisation at that energy scale. I.e. your effective theory is still applicable. Here I must insert a nitpick, it isn’t that “viewing gravity as a “field” like the electromagnetic field(EM)leads to an infinite set of infinities in the calculations that cannot be transformed into finite quantities.” It is a set that, like renormalization of quantum field theory on all scales, always is infinite and must be affixed values from observation. But for gravity when you approach the Planck scale the set of finite value observables you need tend towards an infinity of them (and you lose control of the attempt to achieve a meaningful theory).
Now, we have always known that the analogy to the tool of geodesics of classical general relativity is the tools of field lines in other classical field theories, the difference being having a tensor vs a vector field. If the latter is pure math, why wouldn’t we expect the former to be that as well? In fact a path integral formulation of gravity would have particles follow volume filling distributions with the geodesics as the most dense paths in likelihood space. And with flat space the relativistic Lorentzian signature that preserves universal laws is a path integral factor of space time, while the potential added gravity field effect is a correction term in the state transition amplitudes [c.f. Nobel Laureate Wilczek’s Core Theory].
There may be no principle problem here at all, as was actively hoped by earlier generations Theory Of Everything physicists for such reasons that singularities may pin some parameter values. Maybe quantum field theory is such theory, giving a finite “tower” of effective theories. [And the parameter values may in large – apart from the shared ones like the universal speed limit – be set by Weinberg’s “anthropic” multiverse. In fact, the recent BOSS galaxy survey collaboration short listed it as the simplest theory explaining the low value of the vacuum energy density, consistent with having quantum field renormalization theory realize the effective theories anyway.] But of course YMMV, and I’m certainly integrating this based on my current bias.
Perhaps I shouldn’t say that classical field lines are math as they have physical character – though they simplify the math – but point was that they are tools and has no real existence.
Also, the BOSS survey reference is the recently released 20 year summary IV, with the cosmological summary paper (among 20+ papers simultaneously published on arxiv),
Ha, we can see that there is a large hole (or too small) in “alternative gravity” theories.
I haven’t access to the paper yet. But the abstract says:
“We show analytically that spacetimes that deviate from the Kerr metric but satisfy weak-field tests can lead to large deviations in the predicted black-hole shadows that are inconsistent with even the current EHT measurements. … We show that the shadow-size measurements place significant constraints on deviation parameters that control the second post-Newtonian and higher orders of each metric and are, therefore, inaccessible to weak-field tests.”
They claim it is a strong-field test, though a black hole that size doesn’t have much gravity strength at the event horizon – it’s just that light can no longer get out against the “flow” of space into the hole – and the shadow covers a larger volume still. It will be interesting to read the paper, is it a principle strong-field test or did it in fact show strong-field effects?
“Einstein’s robust theory remains mathematically irreconcilable with quantum mechanics”.
That is perhaps a misleading way to state the situation, black holes physics show that there is consistency between general relativity and quantum mechanics on the Planck scale. And it is just part of the constraint that these results make, they also reject various “modified gravity” theories.
The part where the classical general relativity theory is fundamentally not a quantum physics theory is the part that is exciting though. And it seems the scientists on the case is moving on from the “modified alternatives” – who where mostly excluded by the binary neutron star merger multimessenger observations anyway – towards more exclusively the ultimate goal of a quantum theory.