
Researchers have moved a step closer to harnessing fusion energy by showing how imaging enables better testing of components for devices. Credit: Swansea University
Harnessing nuclear fusion, which powers the sun and stars, to help meet earth’s energy needs, is a step closer after researchers showed that using two types of imaging can help them assess the safety and reliability of parts used in a fusion energy device.
Scientists from Swansea University, Culham Center for Fusion Energy, ITER in France, and the Max-Planck Institute of Plasma Physics in Germany paired x-ray and neutron imaging to test the robustness of parts.
They found that both methods yield valuable data which can be used in developing components.
The sun is a shining example of fusion in action. In the extremes of pressure and temperature at the center of the sun atoms travel fast enough to fuse together, releasing vast amounts of energy. For decades, scientists have been looking at how to harness this safe, carbon-free, and virtually limitless source of energy.

These are three sample types used for this work: (left) ITER reference monoblock (ITER_MB), (center) Culham Center for Fusion Energy thermal break concept monoblock (CCFE_MB), and (right). Credit: Llion Evans, Swansea University
One major obstacle is the staggering temperatures that components in fusion devices have to withstand: up to 10 times the heat of the center of the sun.
One of the main approaches to fusion, magnetic confinement, requires reactors which have some of the greatest temperature gradients on earth, and potentially in the universe: plasmas reaching highs of 150 million °C (270 million °F) and the cryopump, which is only meters away, as low as -269 °C (-452 °F).
It is critical that researchers can test — non-destructively — the robustness of engineering components that must function in such an extreme environment.
The research team focused on one critical component, called a monoblock, which is a pipe carrying coolant. This was the first time the new tungsten monoblock design has been imaged by computerized tomography. They used ISIS Neutron and Muon Source’s neutron imaging instrument, IMAT.
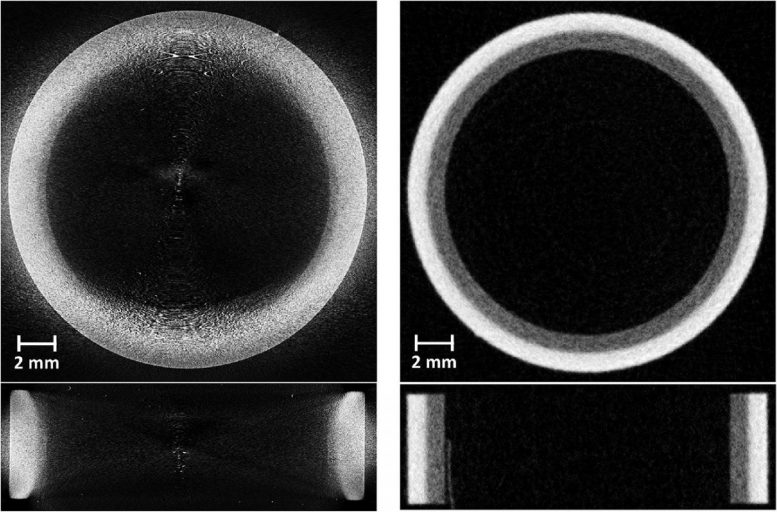
This is an example of cross-sectional tomography data slices from the xy (top) and xz (bottom) planes for the ITER_MB_ROI sample with a comparison of X-ray (left) vs. neutron (right) tomography imaging results. Credit: Llion Evans, Swansea University
Dr. Triestino Minniti of the Science and Technology Facilities Council said:
“Each technique had its own benefits and drawbacks. The advantage of neutron imaging over x-ray imaging is that neutrons are significantly more penetrating through tungsten.
Thus, it is feasible to image samples containing larger volumes of tungsten. Neutron tomography also allows us to investigate the full monoblock non-destructively, removing the need to produce “region of interest” samples”
Dr. Llion Evans of Swansea University College of Engineering said:
“This work is a proof of concept that both these tomography methods can produce valuable data. In the future, these complementary techniques can be used either for the research and development cycle of fusion component design or in quality assurance of manufacturing.”
The next step is to convert the 3D images produced by this powerful technique into engineering simulations with micro-scale resolution. This technique, known as the image-based finite element method (IBFEM), enables the performance of each part to be assessed individually and accounts for minor deviations from design caused by manufacturing processes.
Publication: “Comparison of X-ray and neutron tomographic imaging to qualify manufacturing of a fusion divertor tungsten monoblock” by Ll. M. Evans, T. Minnitic, M. Fursdona, M. Gorley, T. Barrett, F. Domptail, E. Surrey, W. Kockelmann, A. v. Müllerd, F. Escourbiac and A. Durocher, 24 August 2018, Fusion Engineering and Design. DOI:10.1016/j.fusengdes.2018.06.017









Be the first to comment on "Imaging Techniques Will Help Bring Fusion Energy Closer to Reality"