You’d expect LEGO kits to be somewhat immune from mathematics, but that’s not the case, as Samuel Arbesman of Wired’s Social Dimension demonstrated most recently. However, to start out with, it’s necessary to think about how humans combine things together, in general.
In most cases, our daily objects are made up of smaller pieces that are combined in complicated and diverse ways. This is true whether it’s a circuit that’s made out of resistors and capacitors, or living things, which are made up of cells, neurons, and much more. There is a certain diversity when it comes to putting components together and orchestrating a system. The question that came to Mark Changizi was, does the variety of the pieces grow in tandem with the size of the system or do larger circuits just have more types of pieces? Or do they simply use the same handful of parts, over and over again, to make something more complex?
Changizi’s paper Scaling of Differentiation in Networks: Nervous Systems, Organisms, Ant Colonies, Ecosystems, Businesses, Universities, Cities, Electronic Circuits, and LEGOs, Changizi along with his colleagues set out to further understand this concept. They discovered that each one of the systems in their interdisciplinary list experienced an increase in the number of types of components as the total number of pieces grew. Basically, the larger something is, the more types of building blocks it will use.
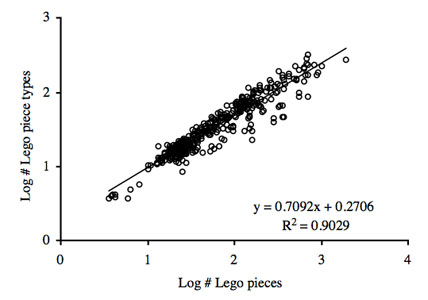
Their dataset includes 389 LEGO sets, in which they examined the distinct types of pieces in relation with the total number of pieces. This relation could be fit onto a power law, in a log-log scale. The curve demonstrates that as the number of pieces in a set grows, so do the number of piece types. The growth is sublinear, meaning that while a larger set uses more piece types, they use progressively less additional piece types. Larger sets actually use fewer types per piece. Basically, the sets become more efficient, using the same pieces that smaller sets use, but in a more complex and diverse way.
The authors used an optimization argument to prove this point, but intuitively, when a system has to do some selecting, it becomes more costly to create new types of pieces. It then makes sense to use the same pieces in a more efficient manner. In the case of LEGO bricks, this is down to some economic factor. This is the first study that examines existing LEGO sets and sees them as systems.
Never miss a breakthrough: Join the SciTechDaily newsletter.
Follow us on Google and Google News.
3 Comments
“Mathematics and LEGOs”?
The plural of LEGO is LEGO, not LEGOs. (But at least you didn’t write “Math and LEGOs”, that would have been too awful.)
I removed the ‘s’ from the title. The original paper uses the term Legos, so at least we properly used all caps for LEGO.
Still love my LEGO, for Danish kids LEGO is one of the top “toys”. Thanks for interesting article.