Researchers report a new, highly unusual, structured-light family of 3D topological solitons, the photonic hopfions, where the topological textures and topological numbers can be freely and independently tuned.
We can frequently find in our daily lives a localized wave structure that maintains its shape upon propagation—picture a smoke ring flying in the air. Similar stable structures have been studied in various research fields and can be found in magnets, nuclear systems, and particle physics. In contrast to a ring of smoke, they can be made resilient to perturbations. This is known in mathematics and physics as topological protection.
A typical example is the nanoscale hurricane-like texture of a magnetic field in magnetic thin films, behaving as particles—that is, not changing their shape—called skyrmions. Similar doughnut-shaped (or toroidal) patterns in 3D space, visualizing complex spatial distributions of various properties of a wave, are called hopfions. Achieving such structures with light waves is very elusive.
Recent studies of structured light revealed strong spatial variations of polarization, phase, and amplitude, which enable the understanding of—and open up opportunities for designing—topologically stable optical structures behaving like particles. Such quasiparticles of light with control of diversified topological properties may have great potential, for example as next-generation information carriers for ultralarge-capacity optical information transfer, as well as in quantum technologies.
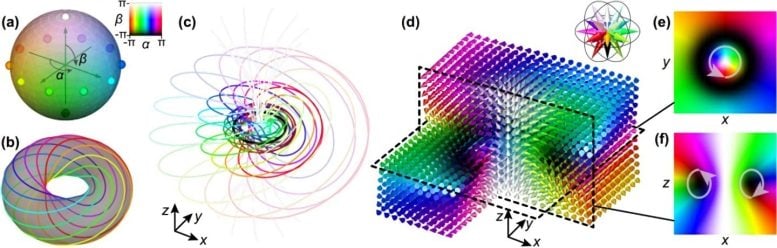
(a) The parameter-space sphere which represents spin: the longitude and latitude degrees (α and β) of a parametric 2-sphere are represented by hue color and its lightness (dark towards the south pole, where spin is down, and bright towards the north pole, where spin is up). Each point on a parametric 2-sphere corresponds to a closed iso-spin line located in a 3D Euclidean space. (b) The lines projected from the selected points of the same latitude β and different longitude α on the hypersphere (highlighted by the solid dots with the corresponding hue colors), form torus knots covering a torus (with different tori corresponding to different β). (c) The real-space visualization of a Hopf fibration as a full stereographic mapping from a hypersphere: torus knots arranged on a set of coaxially nested tori, with each torus corresponding to different latitude β of a parametric 2-sphere. The black circle corresponds to the south pole (spin down) and the axis of the nested tori corresponds to the north pole (spin up) in (a). (d) The 3D spin distribution in a hopfion, corresponding to the isospin contours in (c) with each spin vector colored by its α and β parameters of a parametric sphere in (a) as shown in the insert. (e, f) The cross-sectional view of the spin distribution in (d): (e) xy (z = 0) and (f) yz (x = 0) cross-sections show skyrmion-like structures with the grey arrows marking the vorticity of the skyrmions. Color scale is the same as that corresponding to the spin direction in (d). Credit: Shen et al., doi 10.1117/1.AP.5.1.015001
As reported in the journal Advanced Photonics, collaborating physicists from UK and China recently demonstrated the generation of polarization patterns with designed topologically stable properties in three dimensions, which, for the first time, can be controllably transformed and propagated in free space.
As a consequence of this insight, several significant advances and new perspectives are offered. “We report a new, very unusual, structured-light family of 3D topological solitons, the photonic hopfions, where the topological textures and topological numbers can be freely and independently tuned, reaching far beyond previously described fixed topological textures of the lowest order.” says Yijie Shen of University of Southampton in the UK, the lead author of the paper. “Our results illustrate the immense beauty of light structures. We hope they will inspire further investigations towards potential applications of topological protected light configurations in optical communications, quantum technologies, light-matter interactions, superresolution microscopy, and metrology,” says Anatoly Zayats, professor at King’s College London and project lead.
This work provides a theoretical background describing the emergence of this family of hopfions and their experimental generation and characterization, revealing a rich structure of topologically protected polarization textures. In contrast to previous observations of hopfions localized in solid-state materials, this work demonstrates that, counterintuitively, an optical hopfion can propagate in free space with topological protection of the polarization distribution. The robust topological structure of the demonstrated photonic hopfions upon propagation is often sought in applications.
This newly developed model of optical topological hopfions can be easily extended to other higher-order topological formations in other branches of physics. The higher order hopfions are still a great challenge to observe in other physics communities, from high-energy physics to magnetic materials. The optical approach proposed in this work may provide a deeper understanding of this complex field of structures in other branches of physics.
Reference: “Topological transformation and free-space transport of photonic hopfions” by Yijie Shen, Bingshi Yu, Haijun Wu, Chunyu Li, Zhihan Zhu and Anatoly V. Zayats, 10 January 2023, Advanced Photonics.
DOI: 10.1117/1.AP.5.1.015001









According to the modern discoveries in physics, fundamental forces and elementary particles can be written in terms of a pair of physical and virtual fields.
In physics, topological vortex and anti-vortex fields always appear in pairs. They perfectly reflect the exact symmetry under the simultaneous transformation of parity conservation (P), charge conjugation (C) and time reversal (T).
Topological vortex and anti-vortex field pairs can generate or annihilate at the limit points, and encounter, split or merge at the bifurcation points of the 3-dimensional vector order parameter, and form topological bifurcations by unstable point defects system. This means that the topological bifurcations can be the fundamental understructure of various microscopic particles. Topological vortex and anti-vortex field pairs had all the physical characteristics of elementary particles.
Elementary particles are the foundation of all things. In the presence of dissipation they can form microscopic particles in many forms. Parity conservation (P), charge conjugation (C) and time reversal (T) are the nature feature of elementary particles. These are the essential difference between elementary particles and microscopic particles.