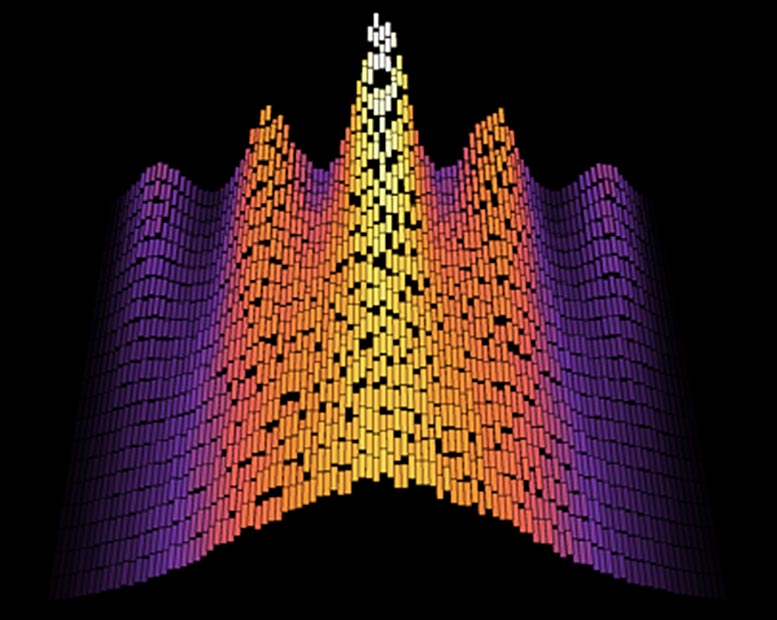
The phonons distribution is complex (upper curves) and then simplifies with time to a Gaussian bell curve (lower curve). Credit: S. Sotiriadis / Freie Universität Berlin
With a clever experiment, physicists have shown that in a one-dimensional quantum system, the initially complex distribution of vibrations or phonons can change over time into a simple Gaussian bell curve. The experiment took place at the Vienna University of Technology, while the theoretical considerations were carried out by a joint research group from the Freie Universität Berlin and HZB.
Quantum physics allows to make statements about the behavior of a wide variety of many-particle systems at the atomic level, from salt crystals to neutron stars. In quantum systems, many parameters do not have concrete values, but are distributed over various values with certain probabilities. Often this distribution takes the form of a simple Gaussian bell curve that is encountered also in classical systems for example the distribution of balls in the Galton box experiment. However, not all quantum systems follow this simple behavior and some might deviate from the Gaussian distribution due to interactions.
Prof. Dr. Jens Eisert, who heads a joint research group on theoretical physics at the Freie Universität Berlin and the Helmholtz-Zentrum Berlin, argues that once interactions are reduced such deviations decay over time and become Gaussian distributed. Now he has been able to substantiate this presumption experimentally.
To do this, the Berlin team worked together with a group of experimental physicists led by Prof. Dr. Jörg Schmiedmayer at the Vienna University of Technology. Schmiedmayer and members of his group, in particular Dr. Thomas Schweigler, prepared a so-called Bose-Einstein condensate: this is a quantum system consisting of several thousand rubidium atoms, which were confined in a quasi-one-dimensional configuration with the help of magnetic fields and cooled near absolute zero (50 nanokelvin).
“The Vienna group created a synthetic quantum system in which the distribution of the phonons can be observed particularly sharply” explains Dr. Marek Gluza, coauthor of the study and postdoc with Jens Eisert. The measurement data initially represent the complex dynamics of the phonons. But the complexity is lost over time and the distribution takes on the shape of a Gaussian bell curve.
“In fact, we can see here how a Gaussian distribution emerges over time. Nature finds a simple solution, all by itself, through its physical laws” comments Jens Eisert.
What is unique about the performed experiment is that as time goes on the system swings back to the more complex distribution, demonstrating that the signatures of a complicated state can be retrieved again. “We know precisely why it swings back and what it depends on”, Gluza explains. “This shows us something about the isolation of the system because the information about the signatures has never left the system.“
Prof. Eisert describes his research result for a wider audience in this short text:
The emergence of simplicity
Nature as we encounter it undeniably features a rich phenomenogy. It is the primary task of physics to describe this phenomelogy. It provides models for it and captures the physical world in terms of basic laws. It aims at understanding how constituents interact and what emergent properties these interactions give rise to. Quantum physics is the best physical theory we have available today to describe nature on a fundamental level. So in one way or the other, these interacting systems will ultimately follow dynamical laws within quantum theory. Given a physical model, that is to say, quantum physics will predict how the system under consideration will evolve in time.
Now strikingly, very simple models happen to describe a wealth of physical situations very well. These are so-called Gaussian states and models. While this may sound abstract, it may be sufficient to say that Gaussian states describe a physical situation at a given time in terms of simple Gaussian distributions. These are distributions of a kind as they are ubiquitous in statistics and in nature, to say the least. Distributions as we used to know from the old note of the ten Deutsche Mark bill. Indeed, physical systems that interact very little can be described by such Gaussian quantum states to a very good approximation. This is all fine, but these insights seem to miss an explanation how quantum systems that have interacted in the past ultimately end up in such Gaussian states. Where does the simplicity come from?
Theoretical work has long predicted notions of “Gaussification,” so physical systems to dynamically move to Gaussian states. In fact, Jens Eisert of the Freie Universität Berlin has suggested similar phenomena theoretically as early as in 2008. But experimental evidence has been missing. Now a team of researchers of the Technical University of Vienna — theoretically supported by a team at the Freie Universität Berlin including Marek Gluza and Spyros Sotiriadis and led by Jens Eisert — has set out to experimentally probe the question how quantum systems ultimately approach Gaussian quantum states. This question is rooted in and is related to the question how ensembles of quantum statistical mechanical would ultimately emerge. Placing atoms cooled to extremely low temperatures on top of a precisely designed chip, the team has been able to approach this long standing question that has already puzzled the forefathers of quantum mechanics under extremely accurate experimental conditions.
Indeed, in this experiment, one sees equilibrium properties as described by Gaussian states to emerge dynamically, accurately monitored in time. After some while, that is to say, one encounters how nature finds itself in a simple situation, one that is captured by simple physical laws: Simplicity emerges dynamically.
Reference: “Decay and recurrence of non-Gaussian correlations in a quantum many-body system” by Thomas Schweigler, Marek Gluza, Mohammadamin Tajik, Spyros Sotiriadis, Federica Cataldini, Si-Cong Ji, Frederik S. Møller, João Sabino, Bernhard Rauer, Jens Eisert and Jörg Schmiedmayer, 18 January 2021, Nature Physics.
DOI: 10.1038/s41567-020-01139-2









Why “prepared a so-called Bose-Einstein condensate:”?
Is there some doubt as to its existence? Should it be called something else?
Sloppy English; or quantum skeptisism?
Makes sense thermodynamically, the system will always tend toward a lower energy state…. unless disturbed by your consciousness! 🙂
Canquantumapplicationabletoproducestaticsolutiontodecayofthebosonparticleintoelectronpairchargedoppositely
It’s the occupancy of space not time that solifiez de escher of repetive natur. Tink de orbit of proton cubes energy in field of vacillating… alternating, volve, revolving, orbiting, gyroscopic, elm currents force carving out space, producing cavity, ultimately establishing d’bloch, primRy circuit, routers, circuits, centrifuges, neutroK, centrifugal force clarity, atmospheric Vbase, ie, greater lighten, lesser mnageighton, sechsitwell, going on its feil, till corresponding, rotates, energy, varnado de plates up to have a good sum.Ner, nice and hence, and chklear. A nuclear anatomy, vant se. Schipper of esper, d love, the xsperit. Delgtx., , ah sacher, eichhrt. Soon treeal.daschit. harrcsee, schumtimes.la pzyzcj. Aschtbull,ahh,,, schlep, eit,schriff, dash mat,schieifflet,.schuni,…zpazzer.descrot,…funit,…ah.basvh.lova.ooops. Daschle menorah.eiiidel’schel,.,schmidt,.uuin,.veil.. finnial.schoot.d’ert. Naschit.banf.oj.
Isch,.eil….,uno!!!.naschball.acha.,rrunmoach..dShtouex.^
Eischl.scheph,.wer., deschiescfell,…culer,.graciazsche,,ruimnee,.. jahh,..scheaveer.,fuchter.daachu,..danzzwer.EREARCHRD.DELIFHEART…EACH PRAESCZ.LOVE.guldfer .zig.a.uscukl,,babi.