
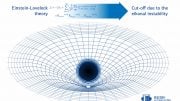
A physicist has developed a formula for calculating Hawking radiation in the vicinity of an Einstein-dilaton-Gauss-Bonnet black hole. Credit: RUDN University
A RUDN University physicist has developed a formula for calculating Hawking radiation on the event horizon of a black hole, which allows physicists to determine how this radiation would be changed with quantum corrections to Einstein’s theory of gravity. This formula will allow researchers to test the accuracy of different versions of the quantum gravity theory by observing black holes, and comprises a step toward the long-sought “grand unification theory” that would connect quantum mechanics and relativity. The article is published in the journal Physical Review D.
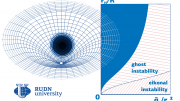
Although Einstein’s gravitation theory corresponds to the recent discovery of gravitation waves, it still leaves open some questions, including the nature of the singularity, dark matter, dark energy, and the question of quantum gravity. Also, even observations of gravity waves do not exclude that alternative gravitation theories may be accurate, and they can be used to describe black holes. Such theories, which include additional quantum components, do not contradict the observed picture of black hole mergers. Calculations made following these theories predict the same behavior of black holes at a great distance from each other, but at the same time, demonstrate important features near the event horizon—the “border” of the black hole from beyond which there is no return.
It is believed impossible to look beyond the event horizon of a black hole because nothing can escape, including particles and radiation. However, Stephen Hawking proved that black holes can “evaporate” by emitting various elementary particles. This means that over time, all the information absorbed by a black hole can disappear, which is contrary to fundamental ideas about information—it is believed that information cannot disappear without a trace. Therefore, alternative gravitation theories, aimed at eliminating this paradox, have become more popular since they could contribute to a quantum gravitation theory.
One of the most promising approaches is the Einstein-dilaton-Gauss-Bonnet theory with dilaton—it applies quantum components as a correction to the Theory of General Relativity.
“The alternative theory we have considered is inspired by the low-energy limit of string theory, the so-called Einstein-dilaton-Gauss-Bonnet theory with dilaton. In addition to the Einstein part, it contains quadratic curvature terms and a scalar field,” Roman Konoplya, a researcher at the Educational and Research Institute of Gravitation and Cosmology of the RUDN University, says.
To describe how a black hole responds to external gravitational perturbations, cosmologists use the concept of quasinormal modes. Modes are oscillations that occur when external actions act on a black hole, the characteristics of which depend on the force of the impact and the parameters of the black hole itself. They are called quasinormal because they fade over time and their amplitude can be measured only for a small period. Such oscillations are usually described using frequency as a complex number, the real part of which is the periodic oscillations, and the imaginary—the decay rate.
The RUDN University physicist, together with Czech Republic scientists Antonina Zinhailo and Zdeněk Stuchlík, studied classical (quasinormal) and quantum (Hawking’s) radiation of test fields on the background of a four-dimensional, spherically symmetric and asymptotically flat black hole in the Einstein-dilaton-Gauss-Bonnet theory with dilaton. They obtained an analytical formula for the eikonal state of quasinormal modes and used it to calculate the quasinormal modes of the test scalar and Maxwell’s fields and estimated the Hawking radiation intensity for the Einstein-dilaton-Gauss-Bonnet black hole.
Text fields are all fields in the vicinity of a black hole because they propagate on its background (for example, a Dirac field or an electromagnetic field). The intensity of the Hawking electromagnetic radiation and the Dirac field proved to be a significantly more sensitive characteristic than its quasinormal spectrum, showing an increase in the rate of energy emission by 57 percent and 48 percent respectively to the fields.
“We obtained an estimate of the intensity of the Hawking evaporation of black holes by taking into account quantum corrections to the geometry of the black hole,” Roman Konoplya concludes.
“Classical radiation (e.g., electromagnetic or other waves) differ from Einstein’s only a few percent, that is, Hawking radiation is a much more sensitive mechanism. Quasinormal modes are the frequencies of classical radiation, which, unlike quantum modes, differ little from the Einstein case. In the future, perhaps by observing the primary black holes that appeared in the early universe, this may clarify our ideas about quantum corrections to gravity.”
Reference: “Quasinormal modes, scattering, and Hawking radiation in the vicinity of an Einstein-dilaton-Gauss-Bonnet black hole” by R. A. Konoplya, A. F. Zinhailo and Z. Stuchlík, 25 June 2019, Physical Review D.
DOI: 10.1103/PhysRevD.99.124042





Trying to stuff in quantum by a hope and a prayer.
Observations upcoming should help to untangle this mess. Hawking radiation according to Hawking does not radiate information.
Stephen Hawking looked like he was being crushed by a black hole in his chair. I dont know physics like he did and one can only wonder if he prayed to be cured or to simply understand black holes and gravity as a whole. Maybe they are one and the same. A previous post states that according to hawking, hawking radiation doesn’t emit information. What if it does, would the crushing weight of a black hole be escapable and the information released be a uniformity.
Yet another mystery: What is RUDN University?