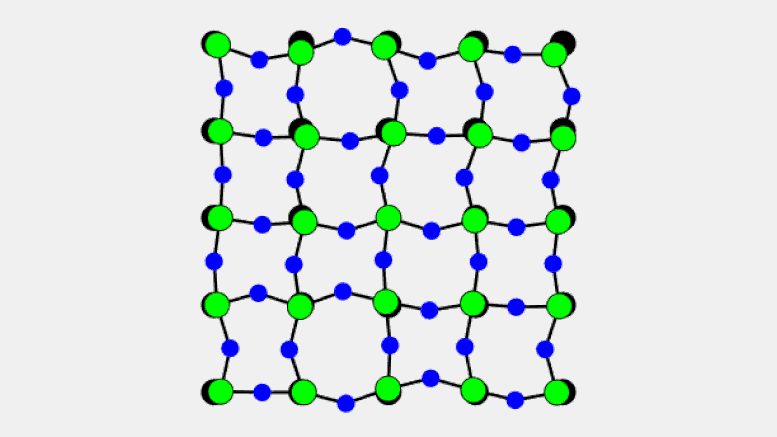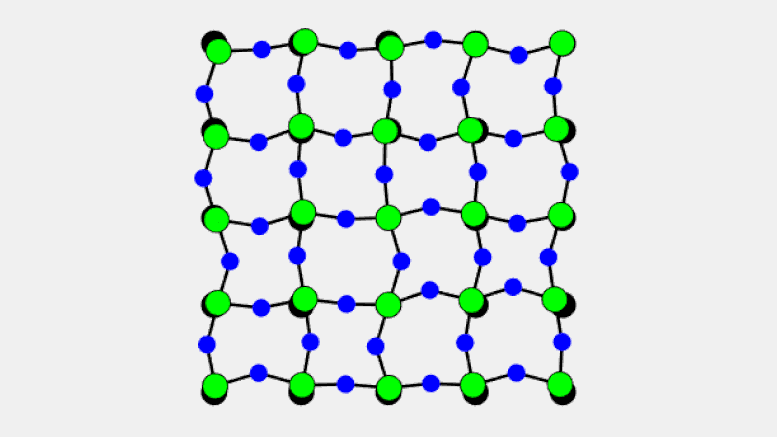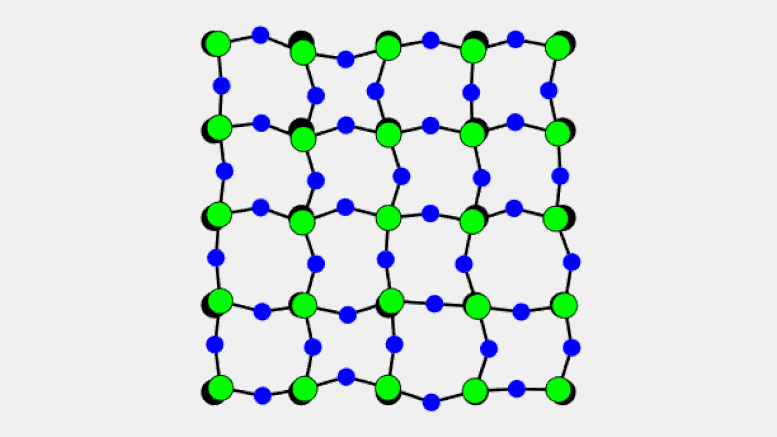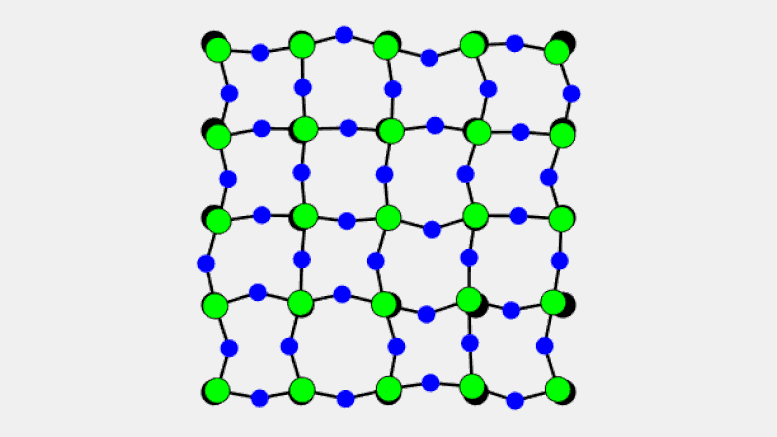
This animation shows how solid crystals of scandium fluoride shrink upon heating. While the bonds between scandium (green) and fluorine atoms (blue) remain relatively rigid, the fluorine atoms along the sides of the cubic crystals oscillate independently, resulting in a wide range of distances between neighboring fluorine atoms. The higher the temperature, the greater the buckling in the sides of the crystals leading to the overall contraction (negative thermal expansion) effect. Credit: Brookhaven National Laboratory
Discovery yields a new quantitative description of unusual behavior relevant to materials used in electronics, medicine, telecommunications, and more.
Scientists at the U.S. Department of Energy’s Brookhaven National Laboratory have new experimental evidence and a predictive theory that solves a long-standing materials science mystery: why certain crystalline materials shrink when heated. Their work, just published today (November 1, 2019) in Science Advances, could have widespread application for matching material properties to specific applications in medicine, electronics, and other fields, and may even provide fresh insight into unconventional superconductors (materials that carry electric current with no energy loss).
The evidence comes from precision measurements of the distances between atoms in crystals of scandium fluoride (ScF3), a material known for its unusual contraction under elevated temperatures (also known as “negative thermal expansion”). What the scientists discovered is a new type of vibrational motion that causes the sides of these cube-shaped, seemingly solid crystals to buckle when heated, thus pulling the corners closer together.
“Normally as something heats up, it expands,” said Brookhaven physicist Igor Zaliznyak, who led the project. “When you heat something up, atomic vibrations increase in magnitude, and the overall material size increases to accommodate the larger vibrations.”

Igor Zaliznyak, a physicist in Brookhaven Lab’s Condensed Matter Physics and Materials Science Division (right), led a team of scientists including Alexei Tkachenko of the Lab’s Center for Functional Nanomaterials (left) to decipher the mechanism underlying scandium fluoride’s ability to shrink upon heating. Credit: Brookhaven National Laboratory
That relationship, however, doesn’t hold for certain flexible materials, including chainlike polymers such as plastics and rubber. In those materials, increasing heat increases vibrations only perpendicular to the length of the chains (picture the sideways vibrations of a plucked guitar string). Those transverse vibrations pull the ends of the chains closer together, resulting in overall shrinkage.
But what about scandium fluoride? With a solid, cubic crystalline structure, it looks nothing like a polymer—at least at first glance. In addition, a widespread assumption that the atoms in a solid crystal have to maintain their relative orientations, no matter what the crystal size, left physicists confounded to explain how this material shrinks when heated.
Neutrons and a dedicated student to the rescue
A group from the California Institute of Technology (Caltech) was using one method to explore this mystery at the Spallation Neutron Source (SNS), a DOE Office of Science user facility at Oak Ridge National Laboratory. Measuring how beams of neutrons, a type of subatomic particle, scatter off the atoms in a crystal can give valuable information about their atomic-scale arrangement. It’s particularly useful for lightweight materials like fluorine that are invisible to x-rays, Zaliznyak said.
Hearing about this work, Zaliznyak noted that his colleague, Emil Bozin, an expert in a different neutron-scattering analysis technique, could probably advance understanding of the problem. Bozin’s method, known as “pair distribution function,” describes the probability of finding two atoms separated by a certain distance in a material. Computational algorithms then sort through the probabilities to find the structural model that best fits the data.

Scientists used neutron scattering at the Spallation Neutron Source at Oak Ridge National Laboratory to investigate why certain crystalline materials shrink when heated. Credit: Oak Ridge National Laboratory
Zaliznyak and Bozin paired up with the Caltech team to collect data at SNS using Caltech’s ScF3 samples to track how the distances between neighboring atoms changed with increasing temperature.
David Wendt, a student who began a Brookhaven Lab High School Research Program internship in Zaliznyak’s lab following his sophomore year in high school (now a freshman at Stanford University), handled much of the data analysis. He continued working on the project throughout his high-school days, earning the position of the first author on the paper.
“David basically reduced the data to the form that we could analyze using our algorithms, fitted the data, composed a model to model the positions of the fluorine atoms, and did the statistical analysis to compare our experimental results to the model. The amount of work he did is like what a good postdoc would do!” Zaliznyak said.
“I am very grateful for the opportunity Brookhaven Lab provided me to contribute to original research through their High School Research Program,” Wendt said.
Results: “soft” motion in a solid
The measurements showed that the bonds between scandium and fluorine don’t really change with heating. “In fact, they expand slightly,” Zaliznyak said, “which is consistent with why most solids expand.”
But the distances between adjacent fluorine atoms became highly variable with increasing temperature.
“We were looking for evidence that the fluorine atoms were staying in a fixed configuration, as had always been assumed, and we found quite the opposite!” Zaliznyak said.

Additional coauthors on the study included (from left) Kate Page, formerly of Oak Ridge National Laboratory, Brookhaven Lab physicist Emil Bozin, and ORNL instrument scientist Joerg Neuefeind. Credit: Genevieve Martin/Oak Ridge National Laboratory
Alexei Tkachenko, an expert in the theory of soft condensed matter at Brookhaven Lab’s Center for Functional Nanomaterials (another Office of Science user facility) made essential contributions to the explanation for this unexpected data.
Since the fluorine atoms appeared not to be confined to rigid positions, the explanation could draw on a much older theory originally developed by Albert Einstein to explain atomic motions by considering each individual atom separately. And surprisingly, the final explanation shows that heat-induced shrinkage in ScF3 bears a remarkable resemblance to the behavior of soft-matter polymers.
“Since every scandium atom has a rigid bond with fluorine, the ‘chains’ of scandium-fluoride that form the sides of the crystalline cubes (with scandium at the corners) act similar to the rigid parts of a polymer,” Zaliznyak explained. The fluorine atoms at the center of each side of the cube, however, are unrestrained by any other bonds. So, as temperature increases, the “underconstrained” fluorine atoms are free to oscillate independently in directions perpendicular to the rigid Sc-F bonds. Those transverse thermal oscillations pull the Sc atoms at the corners of the cubic lattice closer together, resulting in shrinkage similar to that observed in polymers.
Thermal matching for applications
This new understanding will improve scientists’ ability to predict or strategically design a material’s thermal response for applications where temperature changes are expected. For example, materials used in precision machining should ideally show little change in response to heating and cooling to maintain the same precision across all conditions. Materials used in medical applications, such as dental fillings or bone replacements, should have thermal expansion properties that closely match those of the biological structures in which they are embedded (think how painful it would be if your filling expanded while your tooth contracted when drinking hot coffee!). And in semiconductors or undersea fiber-optic transmission lines, the thermal expansion of insulating materials should match that of the functional materials to avoid impeding signal transmission.
Zaliznyak notes that an underconstrained open framework architecture like that in ScF3 is also present in copper-oxide and iron-based superconductors—where crystal lattice vibrations are thought to play a role in these materials’ ability to carry electric current with no resistance.
“The independent oscillation of atoms in these open-framework structures may contribute to these materials’ properties in ways we can now calculate and understand,” Zaliznyak said. “They might actually explain some of our own experimental observations that still remain a mystery in these superconductors,” he added.
“This work profoundly benefitted from the important advantages of the DOE national laboratories—including unique DOE facilities and our ability to have long-time-span projects where important contributions accumulate over time to culminate in a discovery,” Zaliznyak said. “It represents the unique confluence of different expertise among the coauthors, including a dedicated high-school student intern, which we were able to integrate synergistically for this project. It would not have been possible to successfully carry out this research without the expertise provided by all the team members.”
###
Reference: “Entropic elasticity and negative thermal expansion in a simple cubic crystal” by David Wendt, Emil Bozin, Joerg Neuefeind, Katharine Page, Wei Ku, Limin Wang, Brent Fultz, Alexei V. Tkachenko and Igor A. Zaliznyak, 1 November 2019, Science Advances.
DOI: 10.1126/sciadv.aay2748
Brookhaven Lab’s role in this work was funded by the DOE Office of Science.
Brookhaven National Laboratory is supported by the U.S. Department of Energy’s Office of Science. The Office of Science is the single largest supporter of basic research in the physical sciences in the United States and is working to address some of the most pressing challenges of our time.








Be the first to comment on "The Fascinating Secret Behind Crystals That Shrink When Heated"