
A fractal image generated from the Mandelbrot Set.
In mathematics, simple equations can generate a complex evolution in time and intriguing patterns in space. One famous example of this is the Mandelbrot set, named after the French-American mathematician of Polish origin, Benoit B. Mandelbrot (1924-2010), the most studied fractal. This set is based on a single quadratic equation with only one parameter and one variable. The fascinating fractal patterns of the Mandelbrot set have attracted attention far beyond mathematics.
An article by Ralph Andrzejak, entitled “Chimeras confined by fractal boundaries in the complex plane,” forms part of a special edition of the journal Chaos in memory of Russian professor Vadim S. Anishchenko, (1943-2020), published on May 3, 2021. Andrzejak is head of the Nonlinear Time Series Analysis Group at the UPF Department of Information and Communication Technologies (DTIC). The work generalizes the Mandelbrot set for four quadratic equations. The figure shown below is an example of the patterns generated through this approach.
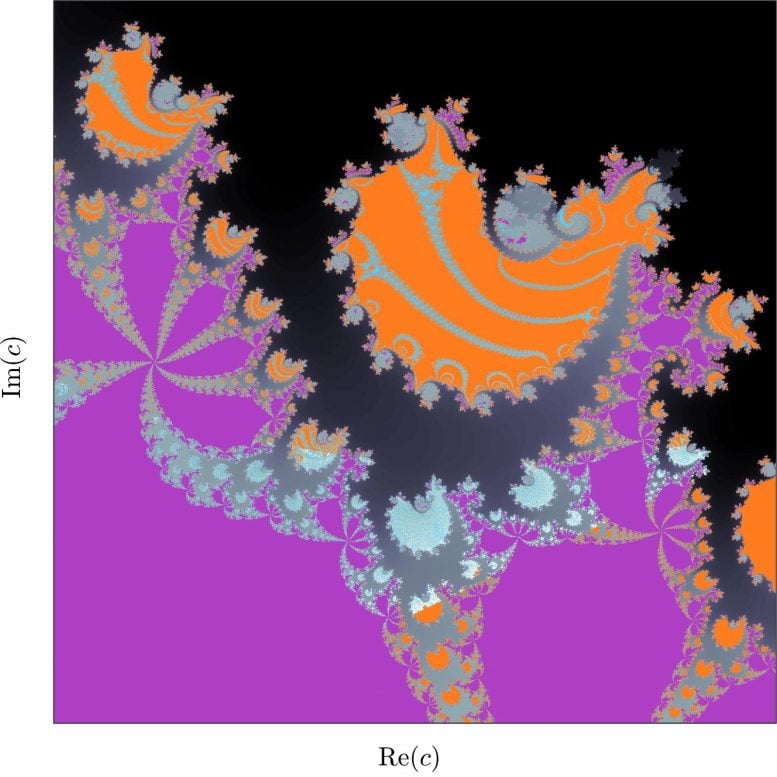
Fractal patterns generated by a set of four quadratic equations. Grey colors indicate divergence to infinity. Non-grey colors code different states of synchronization. Credit: UPF
A journey through many orders of magnitude
Andrzejak notes that “the complexity of fractal patterns can be seen when we get closer to increasingly small details,” which the author illustrates in the image below. He explains the image by saying that “globally, the pattern shown in the top left panel of the figure resembles Mandelbrot’s classic set. However, as soon as we inspect the details, we can see patterns that cannot be found in the Mandelbrot set. To see these details better, we magnify the square to produce the next panel.”

“Iterative zoom in fractal patterns. From left to right and top to bottom, subsequent panels magnify the squares of the corresponding previous panels. The first figure above appears again, here as the fifth step in magnification. Credit: UPF
The author uses a comparison to emphasize that these patterns are indeed at many orders of magnitude. He states that “the zoom applied to the twelve panels that make up the image corresponds to blowing up an atom to the size of an SUV car.” “As we zoom in, increasing the size of the image, we see that there is a rich variety of aesthetically intriguing forms and shapes. The patterns we have discovered may seem less filigree and less ordered, but they can be more varied than those found in the Mandelbrot set.”
Interaction of fractals and synchronization
But there is more than fractal patterns to approach Andrzejak’s proposal. As the author uses four equations instead of one, he has also been able to study synchronization within these fractal patterns. How can we understand this? Andrzejak explains by saying “the Mandelbrot set is based on one equation with one parameter and one variable. We can imagine this variable as a small ball moving on the surface of a large round table. What happens to this ball depends on the parameter of the equation. For some values of this parameter, the ball moves and is always on the table. The set of all these parameter values for which the ball remains on the table is what defines the Mandelbrot set. On the contrary, for the remaining parameter values, the ball falls from the table at some point in time.”
“If we study the basic mechanisms of partial synchronization in very simple models, this can help understand how it is established and how it can be kept stable in such complex systems as the human brain”
Andrzejak continues by saying that “one might think that the four equations we are using describe the movement of not only one, but four balls on the table surface. Since the equations are connected, the balls cannot move freely. However, they attract each other, like the sun, Earth and moon attract each other through gravity.” The researcher adds that “as a result of this attraction, the four balls can show various forms of synchronization. The two extremes are: The four balls move together along the same paths or each ball follows its own path.” Andrzejak then stresses that “most importantly, beyond these extremes, is finding so-called partial synchronization. For example, two balls can move in sync together, while the other two balls remain unsynchronized from this movement. This particular state of partial synchronization is called the chimera state,” hence the title of the article.
A matter of great importance for the dynamics of the real world
If we ask ourselves whether the mathematical model in question can be relevant to the dynamics of the real world, Andrzejak responds “Yes. Absolutely. The best example is the brain. If all our neurons synchronized or went out of sync, our brain could no longer do its job. Our brain can only work properly if some neurons synchronize while other neurons remain out of sync. Partial synchronization is essential for the brain to work properly.” The author relates this to his work saying: “we demonstrate how it is possible to establish partial synchronization in a very simple model and, moreover, we show how this partial synchronization is confined within the fractal limits through full synchronization and desynchronization.” The author concludes: “If we study the basic mechanisms of partial synchronization in very simple models, this can help understand how it is established and how it can be kept stable in such complex systems as the human brain”
Reference: “Chimeras confined by fractal boundaries in the complex plane ” by Ralph G. Andrzejak, 3 May 2021, Chaos.
DOI: 10.1063/5.0049631








… is there a self similar and emergent property of zoom?…
Freaking reason allow common truth age leval
OK