
Example of a cross-section of K3 surface in 3-space, similar to a model Utah State University and University of Missouri-St. Louis mathematicians used to examine string dualities between F-theory and heterotic theory in eight dimensions. Credit: USU
Thomas Hill and Andreas Malmendier of Utah State University explore a string duality between F-theory and heterotic string theory in eight dimensions.
Simply put, string theory is a proposed method of explaining everything. Actually, there’s nothing simple about it. String theory is a theoretical framework from physics that describes one-dimensional, vibrating fibrous objects called “strings,” which propagate through space-time and interact with each other. Piece by piece, energetic minds are discovering and deciphering fundamental strings of the physical universe using mathematical models. Among these intrepid explorers are Utah State University mathematicians Thomas Hill and his faculty mentor, Andreas Malmendier.
With colleague Adrian Clingher of the University of Missouri-St. Louis, the team published findings about two branches of string theory in the paper, “The Duality Between F-theory and the Heterotic String in D=8 with Two Wilson Lines,” in the August 7, 2020, online edition of Letters in Mathematical Physics.
“One important feature of string theories is that these theories require extra dimensions of space-time for mathematical consistency,” says Malmendier, associate professor in USU’s Department of Mathematics and Statistics. “However, not every way of handling these extra dimensions, also called ‘compactification’, produces a model with the right properties to describe nature.”
For so-called eight-dimensional compactification of a string theory model referred to as F-theory, he says, the extra dimensions must be shaped like a K3 surface.
“We studied a special family of K3 surfaces – compact, connected complex surfaces of dimension 2, which are important geometric tools for understanding the symmetries of physical theories,” says Hill, who graduated from USU’s Honors Program with a bachelor’s degree in mathematics in 2018 and completed a master’s degree in mathematics this past spring. “In this case, we were examining a string duality between F-theory and heterotic string theory.”
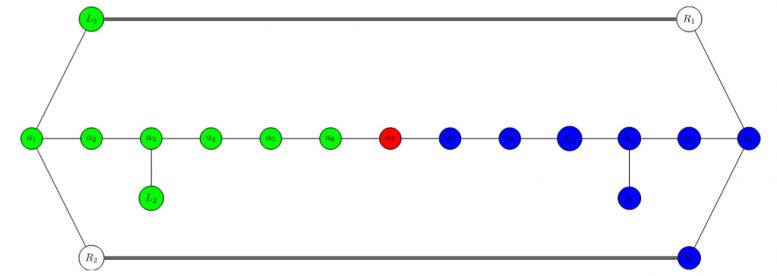
Using an abstract graph, Utah State University researchers identify divisors within each K3 surface to examine varied symmetries. The different Jacobian elliptic fibrations correspond to specific colors of a connected subset of the nodes of the graph. The symmetries of the graph and the possible colorings of the nodes are crucial to understanding the symmetries of the underlying physical theories. Credit: Malmendier/Hill, USU
Hill says the team found four unique ways to slice the K3 surfaces in a particularly useful way, known as Jacobian elliptic fibrations. Fibrations, he says, are formations of torus-shaped fibers supported by the K3 surfaces.
“You can think of this family of surfaces as a loaf of bread and each fibration as a ‘slice’ of that loaf,” Malmendier says. “By examining the sequence of slices, we can visualize, and better understand, the entire loaf.”
Hill says an important part of this research involves identifying certain geometric building blocks, called “divisors”, within each K3 surface.
“Using these divisors, crucial geometric information about the K3 surface is then encoded in an abstract graph,” he says. “This process enables us to investigate symmetries of the underlying physical theories demonstrated by the graph.”
The undertaking described in the paper, Malmendier says, represents hours of painstaking “paper and pencil” work to prove theorems of each of the four fibrations, followed by pushing each theorem through difficult algebraic formulas.
“For the latter part of this process, we used Maple Software and the specialized Differential Geometry package developed at USU, which streamlined our computational efforts,” he says.
The team’s efforts were bolstered by specialized Maple Software libraries developed by USU mathematics professor Ian Anderson and USU physics professor Charlie Torre, as well as efforts by Hill in expanding this library, starting during his undergraduate years.
“This paper represents the ‘grand finale’ of Thomas (Hill)’s achievements here at Utah State,” Malmendier says. “As an undergrad, he honed his software and programming skills and carried this expertise into his master’s program, where he developed expertise in K3 surfaces. Finally, in this publication, he tackles a very complex classification problem. It’s truly exceptional for a master’s student.”
Hill advances this fall to a doctoral program in mathematics, with an emphasis in algebraic geometry, at the University of Utah.
“During his undergraduate career, Thomas was awarded an Undergraduate Research and Creative Opportunities (URCO) grant and was also named a 2017 Goldwater Scholar,” Malmendier says. “In 2018, he received the Honors Program’s Joyce Kinkead Award for Outstanding Honors Capstone Thesis. This past spring, Thomas received an honorable mention during the 2020 National Science Foundation Graduate Research Fellowship Program search.”
In addition to his academic accolades, Malmendier praises Hill’s teaching accomplishments.
“Thomas began working as a teaching assistant for Calculus III with me during his undergrad years,” Malmendier says. “He made short videos explaining vector calculus which, unbeknownst to us at the time, were the perfect preparation for our current pandemic situation.”
In addition, he says, Hill was solely responsible, as a master’s student, for teaching classes in trigonometry and calculus, as well as developing the curriculum for the university’s advanced calculus exam.
“All of Thomas’ research and teaching experiences give him a head start as he advances in his academic career,” Malmendier says.
Reference: “The duality between F-theory and the heterotic string in D=8 with two Wilson lines” by Adrian Clingher, Thomas Hill and Andreas Malmendier, 7 August 2020, Letters in Mathematical Physics.
DOI: 10.1007/s11005-020-01323-8







… In order to unite the small scale and large scale, some measurements need to be taken. Some would say that those steps would lead toward do the world of no strings what so ever, but I don’ know that.
One thing that is strange is the fact that gravity is bit different than other forces, this should lead to the united force for dark matter and ordinary matter, like there is some part where we have intersection, and some where there is no intersection…
… Another thing is the dimension at a small level, could it bi 1D and then morphing to higher dimensions, that would provide much logic for the principle of uncertainty, that was so hated by AA…
… And how time cuts at 1D with high speed would be really obvious now…
So, could it be by, by, by string theory, welcome the new string theory of rally everything…
If one looks at spinning sphere theory one finds that a zero dimensional object is one sphere, a one dimensional object is 2 spheres, six spheres is a torus which is 2 dimensional, and the first 3 dimensional object is 42 spheres, the 2nd layer of a cuboctahedron.
Yeah, but stuff get pretty hard if you can project 2d into 1d, or 3d into 2d, some stuff will be lost, like tha thing is leaking in smaller scale but it gets into bigger scale with smaller dimension…