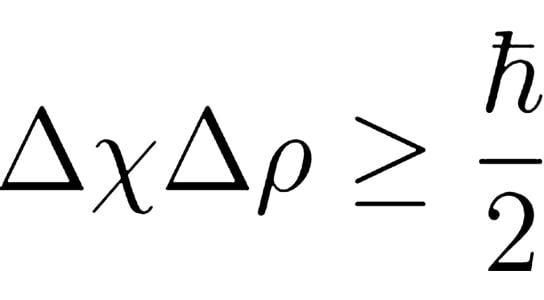
Heisenberg Uncertainty Principle Equation
Students are taught that quantum uncertainty is always in the eye of the beholder, but that principle might have been proven false by a new experiment that measured a quantum system which doesn’t necessarily introduce uncertainty. It overthrows a common classroom explanation of quantum mechanics, but the fundamental limit of what is knowable at the smallest scales remains unchanged.
Scientists published their findings in the journal Physical Review Letters. The Heisenberg Uncertainty Principle states that there is a fundamental limit to what is knowable about a quantum system. The more precisely the observer knows a particle’s position, the less he or she can know about its momentum, and vice versa. The limit is usually expressed as a simple equation.

Heisenberg explains this principle by exposing how a scientist trying to take a photograph of an electron, has to bounce a light particle off its surface. This reveals its position, but imparts energy as well causing it to move.
Aephraim Steinberg of the University of Toronto in Canada and his team of researchers have performed measurements of photons and showed that the act of measuring can introduce less uncertainty that is required by Heisenberg’s principle.
The group didn’t measure position and momentum, but its polarization states. The polarization state along one plane is intrinsically linked to the polarization along the other. By Heisenberg’s principle, there’s a limit to the certainty to which both states can be simultaneously known.
The researchers compared weak measurements with strong measurements multiple times. They found that one measurement of one polarization did not always disturb the other state as much as the uncertainty principle predicted. In the strongest case, the induced fuzziness was little as half of what is predicted by the principle.
There’s still no way that you can know both quantum states accurately at the same time, states Steinberg. However, the experiment shows that the act of measurement doesn’t always cause the uncertainty.
Reference: “Violation of Heisenberg’s Measurement-Disturbance Relationship by Weak Measurements” by Lee A. Rozema, Ardavan Darabi, Dylan H. Mahler, Alex Hayat, Yasaman Soudagar and Aephraim M. Steinberg, 6 September 2012, Physical Review Letters.
DOI: 10.1103/PhysRevLett.109.100404







So Are we Uncertain about the uncertainty? And what about the cat? Is it less dead and Less alive?
What you have to understand is Schrödinger’s cat was never meant as actual experiment, it was always a satirical thought experiment to show how uncertainty would manifest itself in a non-quantum system, and how little sense this interpretation really makes.
Schrödinger would probably actually agree with this news.
The cat died of old age, still in the box 50 years ago.
Your Welcome
You’re*
An Heisenberg hypothesis not is satisfied anytime!
For some weird reason, I could never except the principle, it didn’t make any sense, and off course, at the time the answer was “its because you dont really understand the principle”, suffice to say, neither did they. I do wonder what implications this will have on quantum physics?
Measurement still affects position, its derivative, and energy! This is only suggesting not as much as previously thought.
The principle itself is still valid.
It would be a pity if the principle of superposition lose its foundation.
Always when my girl-friend try to reverse into a parking place i tell her the crash is not her fault because the physics tell that the place MUST blurry away when the impulse of the car is accurate.
Only if you measure it, and not as much as previously thought.
Because if she measured it, the change would be her fault. 🙂
The product of error in observation of both position (x) and momentum (p) measured simultaneously is fixed by an equation of 1/2 of Planck`s constant or even more, in Heisenberg Uncertainty Principle. That means that if the error in position (x) is less , that is when measured accurately, the corresponding error in momentum (p) measurement increases correspondingly to keep the equation correct. In quantum states (i.e.in infinitesimally small states of matter) , classical accurate measurement will not work. This had been beautifully explained by light diffraction rings experiment when light is passed through two adjacent pinholes,where actual travel route of photons through the pinhole number 1 or 2 could not be ascertained. There is still no way that you can know accurately the two quantum states simultaneously, is agreed by the researcher Steinberg in the article. What he had ventured is to find a refined value of polarization states of light in different axis, to minimize errors. He has still not brought the product of (del X by del p) to zero and keeps close to the Heisenberg`s value of 1/2 of Planck`s constant value as far as possible. The inequality still holds good and cannot be thrown out by this article. Thank You.
“The more precisely the observer knows a particle’s position, the less he or she can now about its momentum, “
This has happened because Heisenberg assumed in the derivation of his proof that position and momentum are related by Fourier Transform (FT). His formula thus is an equivalent representation of FT. In electrical engineering it is known as time bandwidth product.
Take a look at the QM chapter by Heisenberg in : “Heisenberg, W., The physical principles of the quantum theory, Translated in English, Eckart, C. & Hoyt, F.C., Dover publications, University of Chicago, (1930).”
“Heisenberg explains this principle by exposing how a scientist trying to take a photograph of an electron, has to bounce a light particle off its surface. This reveals its position, but imparts energy as well causing it to move.”
That does not mean that we cannot use many other available methods to measure both variables. One measurement will give you one equation. But you have two unknowns, position and momentum, so you need at least two measurements to produce two equations to find both variables. In reality you must take millions of measurements at nanoseconds intervals and then solve the equations simultaneously to find the position and momentum at each time instant. Since the particle is moving, some dynamic equations of the particle should also be used along with the measurement equations. Such an integrated approach, based on some least square filtering algorithm, like Kalman Filter, can give you all values with any degree of accuracy.
In a billiard ball game, when you hit the stacked balls by one ball, every ball starts moving. Take a high speed video of the balls, you will be able to see the motions exactly. Same thing will happen when video itself impacts the motion. All you have to consider is – use the motion impact equations. The video, in reality, will still capture the motion. In no engineering you do single measurement to find two unknowns. See the above book for more details.
A similar thing happens when you take a camera photo of a high level yogi. The camera fails to take the photo, but humans can still see the yogi. Take a look at the Yogic Power chapter in the above book. A yogi can become transparent to camera photography. Thus camera technology is not as good as human eyes.
Is it the way we measure that causes the effect, like hitting someone with my car to test their colour would push them in a direction I could not know and ultimately end with them under the car having disappeared from my reality?
Is this actually science, or are a buch or big kids talking about how an obvious knock to an electron would change its momentum? Because that goes without saying.
This disproves nothing. Stop writing fake articles on a science website.