Mathematicians Solve a Knotty Mystery: How To Untangle a Worm Ball

A new study explains how California blackworms can twist and curl around each other by the thousands, forming tightly wound balls and then untangling just as quickly. Credit: Harry Tuazon

California blackworms tangle themselves up by the thousands, then separate in a split second. Their trick may inspire the design of self-detangling materials and fibers.
As anyone who has ever unwound a string of holiday lights or detangled a lock of snarled hair knows, undoing a knot of fibers takes a lot longer than tangling it up in the first place.

This is not so for a wily species of West Coast worm.

Found in marshes, ponds, and other shallow waters, California blackworms (Lumbriculus variegatus) twist and curl around each other by the thousands, forming tightly wound balls over several minutes. In the face of a predator or other perceived threat, the worms can instantly untangle, disassembling the jiggly jumble in milliseconds.

Perplexed by how the wigglers can disentangle such elaborate knots so quickly, MIT mathematicians teamed up with biophysicists at Georgia Tech to study the worms’ knotty behavior. Through experiments and mathematical modeling, the team has now pinned down the mechanism by which the worms tangle up and quickly unwind. Their findings, published today in Science, could inspire designs for fast, reversible, and self-assembling materials and fibers.

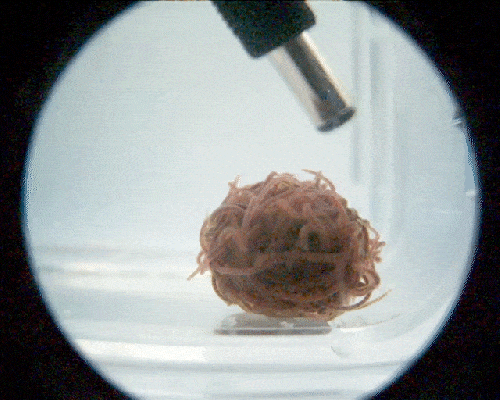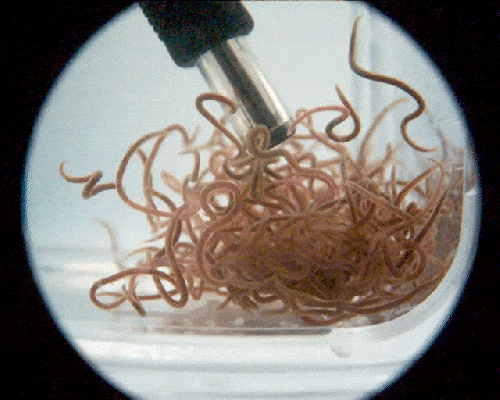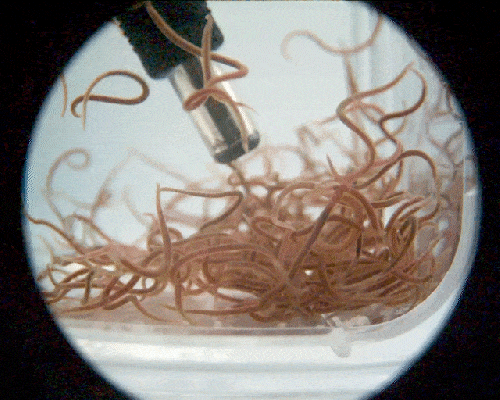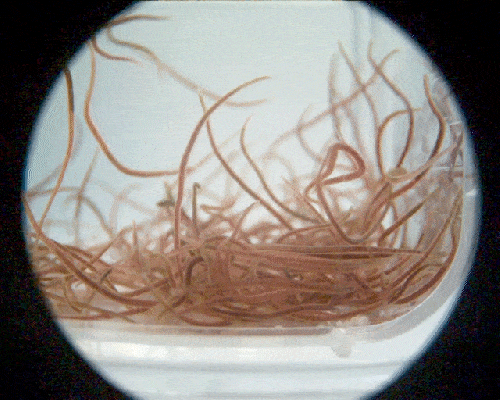
A blob of worms untangling at ultrafast speed. Credit: Georgia Institute of Technology

“We can take inspiration from these worms to think about how we might manipulate polymeric and filamentary systems,” says Vishal Patil, a postdoc at Stanford University, who developed a mathematical model of the worms’ behavior while a graduate student in MIT’s Department of Mathematics. “One could think of engineering active woven fibers that could rearrange when they are clogged or a smart robot that could change its grasp by tangling and untangling.”

Patil’s co-authors on the study are Jörn Dunkel, professor of mathematics at MIT, and co-first author Harry Tuazon, along with Emily Kaufman, Tuhin Chakrabortty, David Qin, and M. Saad Bhamla at Georgia Tech.

Hooked on a tangle

Bhamla’s group studies worms, insects, and other living organisms, and how their behavior can inspire the design of new devices and robotic systems. Tuazon, a PhD student in the lab, was observing California blackworms swimming in a laboratory aquarium when they were struck by the worms’ remarkable tangling and untangling abilities.

The group has previously found that in nature, the worms tangle up as a protective and defensive mechanism. A large knot of worms can prevent interior worms from drying out in drought conditions. A ball of worms can also move as one, collectively crawling along the floor of a lake or pond. When they sense a predator, the worms can untangle in milliseconds, dispersing in many directions.

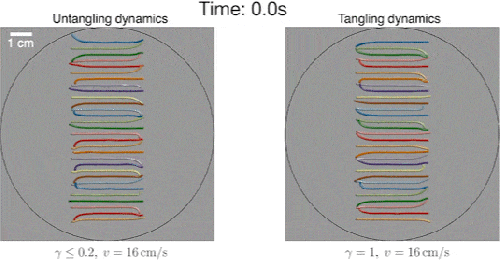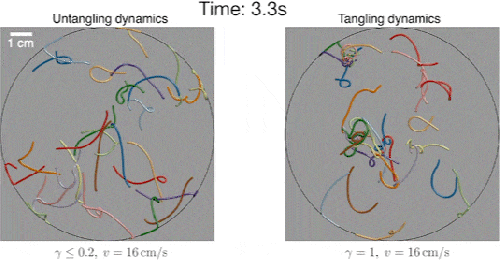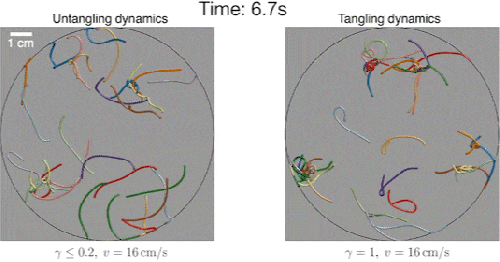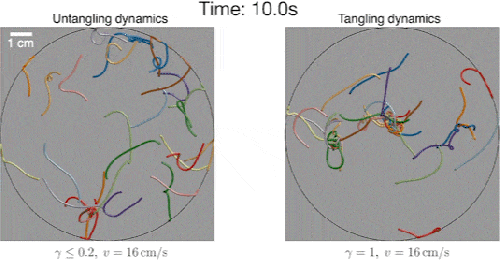
Simulation of worms untangling (left) and tangling (right). Credit: MIT

Wondering what the worms could be doing to get themselves out of such intricate configurations, Bhamla recalled a study by Dunkel and his group at MIT. In that work, the mathematicians devised a model that predicts a knot’s stability, based on the twists and crossings of various knotted segments.

“I saw this study and thought, my goodness, these mathematical principles could be suited to being applied to worms,” says Bhamla, who reached out to Dunkel and Patil to see whether they could shed mathematical insight on the worms’ knotting. Bhamla also sent the mathematicians a few videos taken in the lab of the tangling worms.

“When he showed us those videos, especially of the worms untangling, we were hooked,” Patil says. “We know intuitively it’s really difficult to untangle fibers. The fact that the worms were able to solve that showed that there was something interesting going on with these tangles that we wanted to work out mathematically.”

Dance step

Dunkel and Patil adapted their mathematical codes on knot stability to worm tangling by first studying the behavior of a single worm. They watched Tuazon’s recordings of one worm in a petri dish of water and observed that in response to a perceived threat such as a pulse of ultraviolet light, the worm suddenly corkscrewed, looping to the left, then quickly to the right, again and again.

“That recurrent figure-eight motion suggested to us an unweaving mechanism that could operate to untangle from a knot,” Patil says.

The mathematicians then studied videos of two worms to see if any patterns in their motion guaranteed that the pair would tangle.

“If you just get two fibers together, it’s not clear that they will braid around each other,” Patil says. “Both the tangling and untangling were dynamics we wanted to unpack.”

Surprisingly, they found that the worms tangled up by moving in the same helical motion as untangling. The only difference seemed to be that the two worms tangled by looping in one direction for a longer stretch of time before switching to loop in the other direction, whereas the single worm switched directions quickly, looping left, then right, and back again.

The scientists suspected that the worms tangled and untangled based on how fast they switched their looping direction. The team incorporated these new parameters of helical motion and the speed of loop switching into their existing knot model, which they then used to simulate the behavior of hundreds of computer-generated worms.

“It’s a very minimal model, in which each worm basically runs its own program of helical movements, and how fast they switch directions,” Dunkel says. “You can think of them as having two gears: a slow gear, which allows them to tangle, and a fast gear, which lets them untangle.”

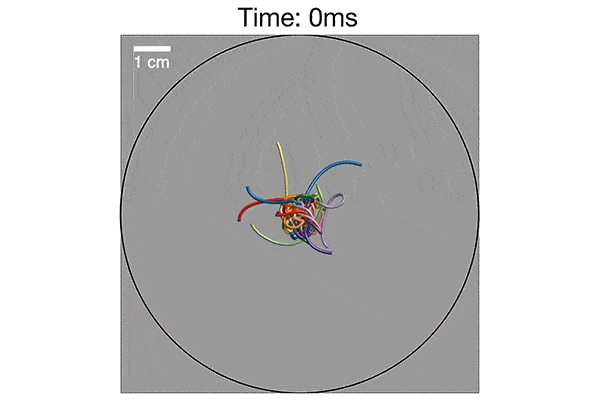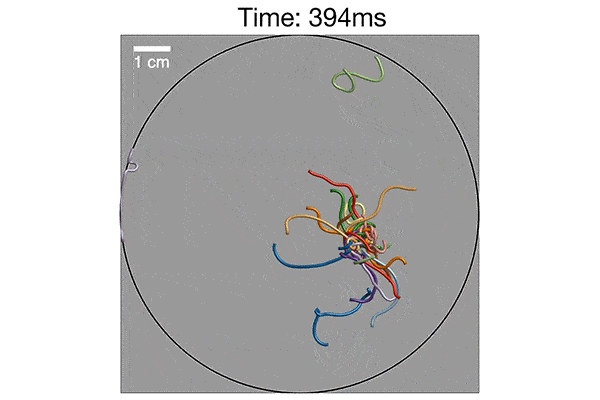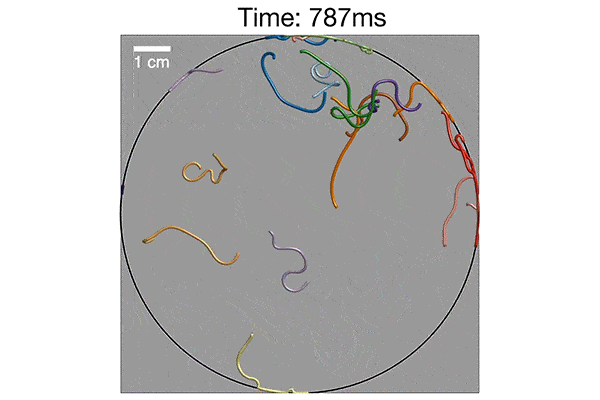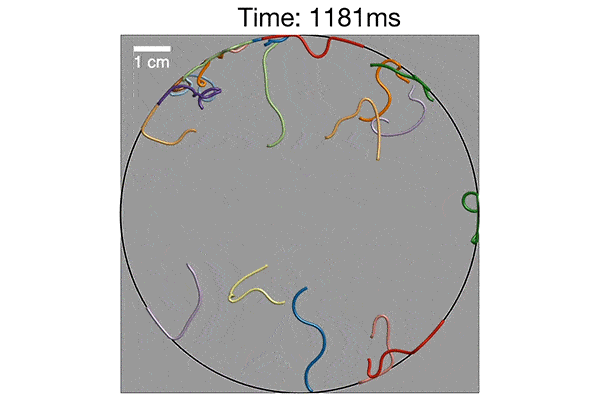
MIT and Georgia Tech researchers have pinned down the pattern by which a knot of worms quickly untangle. Shown here is a mathematical simulation, verified with experiments, that illustrates how worms curve and swirl around each other to disentangle, in about one second. Credit: Georgia Tech

The team simulated numerous scenarios of worm-like fibers and found those that were slower to switch looping directions indeed tangled up in large balls. Fibers that switched quickly from one direction to the other were able to disentangle from a knot.

When they compared their simulations with ultrasound images of actual worms taken at Georgia Tech, the group discovered the pattern of movements in both were the same. Vishal and Dunkel’s mathematical description, involving helical motion and looping speed, accurately predicted the worms’ tangling, and fast untangling.

“We realized this simple dance,” Bhamla says. “The biological circuit is the same. But it’s like the dance music changed, from a slow waltz to Elvis hip-hop, and they suddenly untangle.”

“This study is about the behavior of worms, but it turns out they can be a model system for engineering filamentary matter,” Patil says. “How worms use this tangled state is unique, but we can extract design principles, and engineer systems, based on how we now understand tangles work.”

For more on this research, see Math Behind Wiggly Worm Knots Could Inspire Shapeshifting Robotics.

Reference: “Ultrafast reversible self-assembly of living tangled matter” by Vishal P. Patil, Harry Tuazon, Emily Kaufman, Tuhin Chakrabortty, David Qin, Jörn Dunkel and M. Saad Bhamla, 27 April 2023, Science.
DOI: 10.1126/science.ade7759

This research was supported, in part, by the National Science Foundation and the Sloan Foundation.