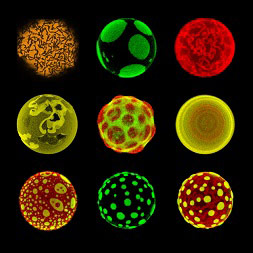
In a virtual computer experiment, researchers discovered information strings exhibiting peculiar properties. Credit: University of Southern Denmark
Newly published research details how a team of scientists used a virtual computer experiment to discover information strings with peculiar properties.
How did life originate? And can scientists create life? These questions not only occupy the minds of scientists interested in the origin of life, but also researchers working with technology of the future. If we can create artificial living systems, we may not only understand the origin of life – we can also revolutionize the future of technology.
Protocells are the simplest, most primitive living systems, you can think of. The oldest ancestor of life on Earth was a protocell, and when we see, what it eventually managed to evolve into, we understand why science is so fascinated with protocells. If science can create an artificial protocell, we get a very basic ingredient for creating more advanced artificial life.
However, creating an artificial protocell is far from simple, and so far no one has managed to do that. One of the challenges is to create the information strings that can be inherited by cell offspring, including protocells. Such information strings are like modern DNA or RNA strings, and they are needed to control cell metabolism and provide the cell with instructions about how to divide.
Essential for life
If one daughter cell after a division has slightly altered information (maybe it provides a slightly faster metabolism), it may be more fit to survive. Therefore it may be selected and an evolution has started.
Now researchers from the Center for Fundamental Living Technology (FLINT), Department of Physics, Chemistry and Pharmacy, University of Southern Denmark, describe in the journal Europhysics Letters, how they, in a virtual computer experiment, have discovered information strings with peculiar properties.
Professor and head of FLINT, Steen Rasmussen, says:
“Finding mechanisms to create information strings are essential for researchers working with artificial life.”
Steen Rasmussen and his colleagues know they face two problems:
Firstly long molecular strings are decomposed in water. This means that long information strings “break” quickly in water and turn into many short strings. Thus it is very difficult to maintain a population of long strings over time.
Secondly, it is difficult to make these molecules replicate without the use of modern enzymes, whereas it is easier to make a so-called ligation. A ligation is to connect any combination of two shorter strings into a longer string, assisted by another matching longer string. Ligation is the mechanism used by the SDU researchers.
“In our computer simulation – our virtual molecular laboratory – information strings began to replicate quickly and efficiently as expected. However, we were struck to see that the system quickly developed an equal number of short and long information strings and further that a strong pattern selection on the strings had occurred. We could see that only very specific information patterns on the strings were to be seen in the surviving strings. We were puzzled: How could such a coordinated selection of strings occur, when we knew that we had not programmed it. The explanation had to be found in the way the strings interacted with each other”, explains Steen Rasmussen.
It is like society
According to Steen Rasmussen, a so-called self-organizing autocatalytic network was created in the virtual pot, into which he and his colleagues poured the ingredients for information strings.
An autocatalytic network is a network of molecules, which catalyze each other’s production. Each molecule can be formed by at least one chemical reaction in the network, and each reaction can be catalyzed by at least one other molecule in the network. This process will create a network that exhibits a primitive form of metabolism and an information system that replicates itself from generation to generation.
“An autocatalytic network works like a community; each molecule is a citizen who interacts with other citizens and together they help create a society”, explains Steen Rasmussen.
This autocatalytic set quickly evolved into a state where strings of all lengths existed in equal concentrations, which is not what is usually found. Further, the selected strings had strikingly similar patterns, which is also unusual.
“We might have discovered a process similar to the processes that initially sparked the first life. We of course don’t know if life actually was created this way – but it could have been one of the steps. Perhaps a similar process created sufficiently high concentrations of longer information strings when the first protocell was created”, explains Steen Rasmussen.
Basis for new technology
The mechanisms underlying the formation and selection of effective information strings are not only interesting for the researchers who are working to create protocells. They also have value to researchers working with tomorrow’s technology, like they do at the FLINT Center.
“We seek ways to develop technology that’s based on living and life-like processes. If we succeed, we will have a world where technological devices can repair themselves, develop new properties and be re-used. For example a computer made of biological materials poses very different – and less environmentally stressful – requirements for production and disposal”, says Steen Rasmussen.
Reference: “Structure and selection in an autocatalytic binary polymer model” by Shinpei Tanaka1, Harold Fellermann and Steen Rasmussen, 14 July 2014, EPL.
DOI: 10.1209/0295-5075/107/28004
arXiv: 1308.6158



PROGRAM QUANTUM LIFE ON WINLIFE 32, YOU MAY THEN ALTER LIFE BY DOING NO HARM AND KEEP COPIES OF YOUR ATTEMPS …. pure zen
you already have a macro-quantum computer program,to use don’t waste it use it. learn how to program with quanta
do a search on SciTech daily for quantum and for qubit, read and digest the comments
The GOLDEN rule is the meaning of life PHI, IT IS ALSO THE RULE OF QUANTUM LIFE
inner-space is the equal and opposite of outer space, we live on an event in 3D SPACE, 4D SPACE IS QUANTUM BOTH ARE SUBJECT TO THE POWER LAW AND EVOLVED FROM IT, an ape is an ape until it mutates to the quantum life…….START GROWING UP ….YOUR IS QUANTUM MIND UNBOUND IT AND SEE IT THROUGH YOUR APE EYES WITH YOUR QUANTUM MIND THAT KNOWS GOOD AND BAD AND HAS A CHOICE TO MAKE….an ape with a quantum MIND is still an ape until it is used YOU ARE THE MISSING LINK.. THINK IT OVER AND BECOME ENLIGHTENED
Hint for the program of Q, I THINK, the quantum is becoming all the torque at the moment……I hope I saw right !!! is correct !!!
Q = NOTHING CAN STOP WHAT IS COMING….NOTHING! QUANTUM PARALLEL TIME TRAVEL TO 4D THROUGH A HOLE IN SPACE that is the PORTAL of EVENT HORIZON, WE WILL BE CHANGED IN THE TWINKLING OF AN EYE, ASCENDED to the the ORIGINAL STATE that WE NEED TO BE RECYCLED IN ORDER to GET THERE, HOW ? A WHITE HOLE. ASCENSION 🌞 HOLE that WAS FORETOLD BY EVERY ANCIENT CULTUREE & ILL GO With THEIR VERSION of TRUTH VERSE ANYTHING the CURRENT PARADIGM SPEEWS 👉🌓👈 QUANTUM PARALLEL UNIVERS, QUANTUM MECHANICS OF NATURE& BIOLOGY