Abstract quantum physics illustration.
Scientists trained a machine learning tool to capture the physics of electrons moving on a lattice using far fewer equations than would typically be required, all without sacrificing accuracy.
A daunting quantum problem that until now required 100,000 equations has been compressed into a bite-size task of as few as four equations by physicists using artificial intelligence. All of this was accomplished without sacrificing accuracy. The work could revolutionize how scientists investigate systems containing many interacting electrons. Furthermore, if scalable to other problems, the approach could potentially aid in the design of materials with extremely valuable properties such as superconductivity or utility for clean energy generation.
The study, by researchers at the Flatiron Institute and their colleagues, was published in the September 23 issue of Physical Review Letters.
“We start with this huge object of all these coupled-together differential equations; then we’re using machine learning to turn it into something so small you can count it on your fingers,” says study lead author Domenico Di Sante. He is an assistant professor at the University of Bologna in Italy and a visiting research fellow at the Flatiron Institute’s Center for Computational Quantum Physics (CCQ) in New York City.
The challenging quantum problem concerns how electrons behave as they move on a gridlike lattice. When two electrons occupy the same lattice site, they interact. Known as the Hubbard model, this setup is an idealization of several important classes of materials and enables scientists to learn how electron behavior gives rise to very sought-after phases of matter, including superconductivity, in which electrons flow through a material without resistance. The model also serves as a proving ground for new methods before they’re unleashed on more complex quantum systems.

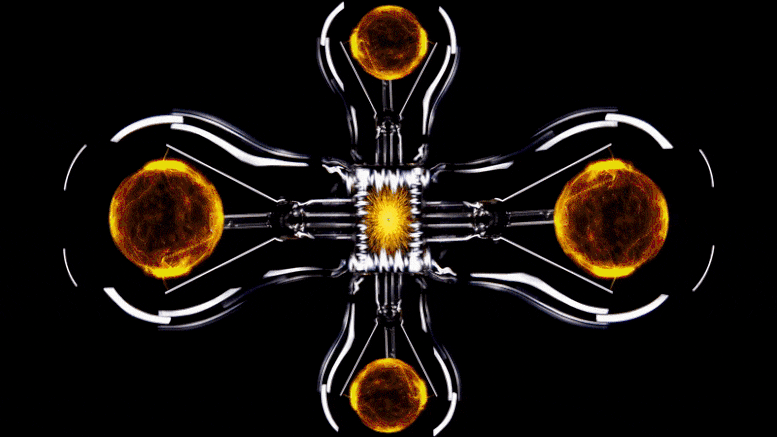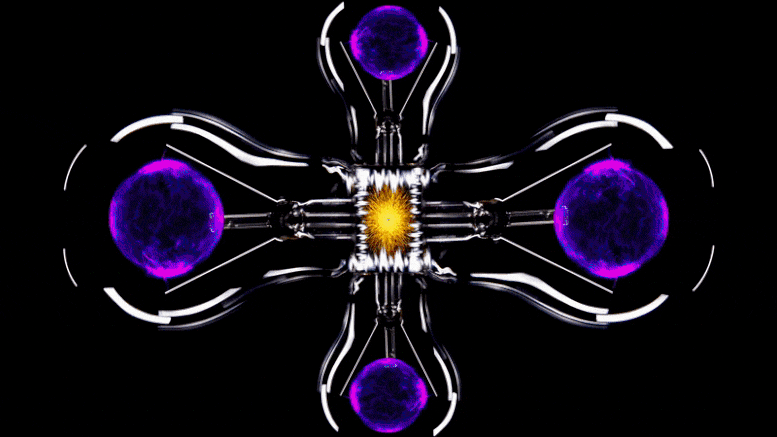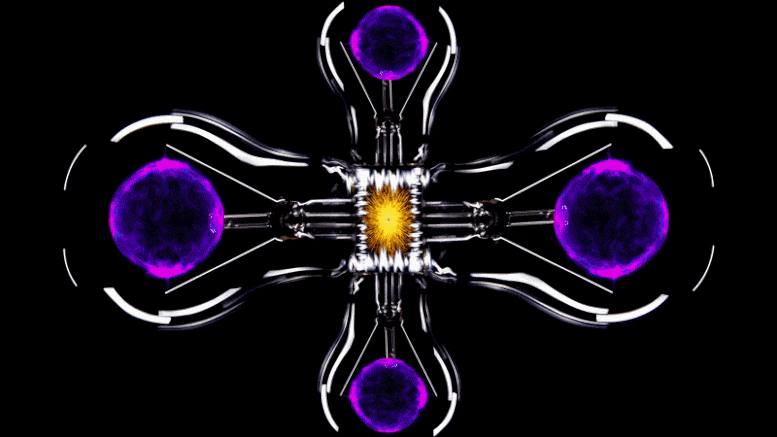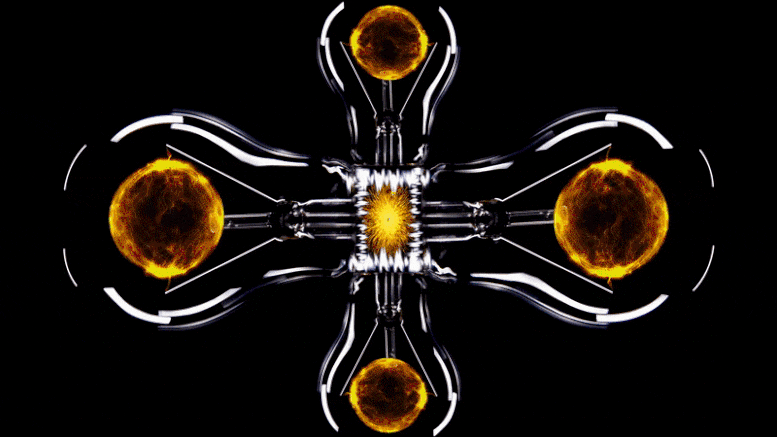
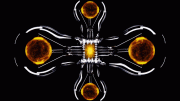
A visualization of a mathematical apparatus used to capture the physics and behavior of electrons moving on a lattice. Each pixel represents a single interaction between two electrons. Until now, accurately capturing the system required around 100,000 equations — one for each pixel. Using machine learning, scientists reduced the problem to just four equations. That means a similar visualization for the compressed version would need just four pixels. Credit: Domenico Di Sante/Flatiron Institute
However, the Hubbard model is deceptively simple. For even a modest number of electrons and cutting-edge computational approaches, the problem requires massive computing power. That’s because when electrons interact, their fates can become quantum mechanically entangled. This means that even once they’re far apart on different lattice sites, the two electrons can’t be treated individually. Therefore, physicists are required to deal with all the electrons at once rather than one at a time. With more electrons, more entanglements crop up, making the formidable computational challenge exponentially harder.
“It’s essentially a machine that has the power to discover hidden patterns. When we saw the result, we said, ‘Wow, this is more than what we expected.’ We were really able to capture the relevant physics..” — Domenico Di Sante
One way of studying a quantum system is by using what’s called a renormalization group. That’s a mathematical apparatus physicists use to look at how the behavior of a system — such as the Hubbard model — changes when researchers modify properties such as temperature or look at the properties on different scales. Unfortunately, a renormalization group that keeps track of all possible couplings between electrons and doesn’t sacrifice anything can contain tens of thousands, hundreds of thousands, or even millions of individual equations that need to be solved. On top of that, the equations are quite tricky: Each represents a pair of electrons interacting.
Di Sante and his colleagues wondered if they could use a machine learning tool known as a neural network to make the renormalization group more manageable. The neural network is like a cross between a frantic switchboard operator and survival-of-the-fittest evolution. First, the machine learning program creates connections within the full-size renormalization group. The neural network then tweaks the strengths of those connections until it finds a small set of equations that generates the same solution as the original, jumbo-size renormalization group. The program’s output captured the Hubbard model’s physics even with just four equations.
“It’s essentially a machine that has the power to discover hidden patterns,” Di Sante says. “When we saw the result, we said, ‘Wow, this is more than what we expected.’ We were really able to capture the relevant physics.”
Training the machine learning program required considerable computational muscle, and the program ran for entire weeks. The good news, Di Sante says, is that now that they have their program coached, they can adapt it to work on other problems without having to start from scratch. He and his collaborators are also investigating just what the machine learning is actually “learning” about the system. This could provide additional insights that might otherwise be hard for physicists to decipher.
Ultimately, the biggest open question is how well the new approach works on more complex quantum systems such as materials in which electrons interact at long distances. In addition, there are exciting possibilities for using the technique in other fields that deal with renormalization groups, Di Sante says, such as cosmology and neuroscience.
Reference: “Deep Learning the Functional Renormalization Group” by Domenico Di Sante, Matija Medvidović, Alessandro Toschi, Giorgio Sangiovanni, Cesare Franchini, Anirvan M. Sengupta and Andrew J. Millis, 21 September 2022, Physical Review Letters.
DOI: 10.1103/PhysRevLett.129.136402
Di Sante co-authored the new study with CCQ guest researcher Matija Medvidović (a graduate student at Columbia University), Alessandro Toschi of TU Wien in Vienna, Giorgio Sangiovanni of the University of Würzburg in Germany, Cesare Franchini of the University of Bologna in Italy, CCQ and Center for Computational Mathematics senior research scientist Anirvan M. Sengupta, and CCQ co-director Andy Millis. Di Sante’s time at the CCQ was supported by a Marie Curie International Fellowship, which encourages transnational scientific collaboration.






Who cares if AI can play great games with math problems! What about climate change and global warming? What about designing a sustainable Nuclear Fusion reactor. We’ll get excited about AI when it can solve some of these real problems. Until then we really don’t need to hear about how well AI plays chess or what great art it can make.
Hi Tony! Deeper our understanding of the electrons and their behavior in the materials is, the better new materials we can create. Concrete problems this novel idea could solve: lower cost batteries for electric cars, better materials for fusion reactor, less power consuming computer circuits … I hope this helps understanding the relevance.
Hi Tony,
AI can’t help solve problems that don’t actually exist. Nuclear was solved in the 60s and it’s only politics that prevent everyone from having access to its cheap energy.
If I have to read an article over and over again, it’s this one. Thanks for the special tips. More please>>>
Hi Tony!! My Dad always told me to try to understand life from another’s perspective and I’m thinking this is one of the instances he meant. Will be looking forward to reading more from you☺️
… Yeah, now is the time for physics falks to bow to new kid in the block…
Someone once told me to try to understand life from another’s perspective and I’m thinking this is one of the instances he meant. Will be looking forward to reading more from you here!!