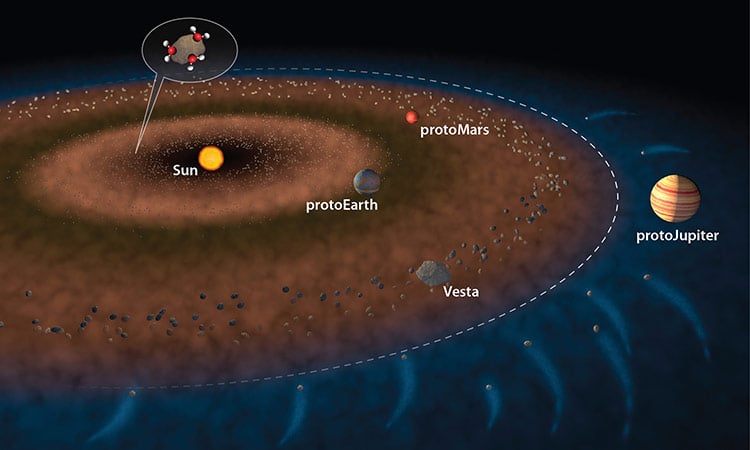
In this illustration of the early solar system, the dashed white line represents the snow line—the transition from the hotter inner solar system, where water ice is not stable (brown) to the outer Solar system, where water ice is stable (blue). Two possible ways that the inner solar system received water are: water molecules sticking to dust grains inside the “snow line” (as shown in the inset) and carbonaceous chondrite material flung into the inner solar system by the effect of gravity from protoJupiter. With either scenario, water must accrete to the inner planets within the first ca. 10 million years of solar system formation. Credit: Jack Cook, Woods Hole Oceanographic Institution
New research from Woods Hole Oceanographic Institution shows that Earth’s water most likely accreted at the same time as the rock, suggesting that Earth received most of its water relatively early from chondrite-like bodies.
Earth is known as the Blue Planet because of its oceans, which cover more than 70 percent of the planet’s surface and are home to the world’s greatest diversity of life. While water is essential for life on the planet, the answers to two key questions have eluded us: where did Earth’s water come from and when?
While some hypothesize that water came late to Earth, well after the planet had formed, findings from a new study led by scientists at the Woods Hole Oceanographic Institution (WHOI) significantly move back the clock for the first evidence of water on Earth and in the inner solar system.
“The answer to one of the basic questions is that our oceans were always here. We didn’t get them from a late process, as was previously thought,” said Adam Sarafian, the lead author of the paper published October 31, 2014, in the journal Science and a MIT/WHOI Joint Program student in the Geology and Geophysics Department.
One school of thought was that planets originally formed dry, due to the high-energy, high-impact process of planet formation, and that the water came later from sources such as comets or “wet” asteroids, which are largely composed of ices and gases.
“With giant asteroids and meteors colliding, there’s a lot of destruction,” said Horst Marschall, a geologist at WHOI and coauthor of the paper. “Some people have argued that any water molecules that were present as the planets were forming would have evaporated or been blown off into space, and that surface water as it exists on our planet today, must have come much, much later—hundreds of millions of years later.”
The study’s authors turned to another potential source of Earth’s water— carbonaceous chondrites. The most primitive known meteorites, carbonaceous chondrites, were formed in the same swirl of dust, grit, ice, and gasses that gave rise to the sun some 4.6 billion years ago, well before the planets were formed.
“These primitive meteorites resemble the bulk solar system composition,” said WHOI geologist and coauthor Sune Nielsen. “They have quite a lot of water in them, and have been thought of before as candidates for the origin of Earth’s water.”
In order to determine the source of water in planetary bodies, scientists measure the ratio between the two stable isotopes of hydrogen: deuterium and hydrogen. Different regions of the solar system are characterized by highly variable ratios of these isotopes. The study’s authors knew the ratio for carbonaceous chondrites and reasoned that if they could compare that to an object that was known to crystallize while Earth was actively accreting then they could gauge when water appeared on Earth.
To test this hypothesis, the research team, which also includes Francis McCubbin from the Institute of Meteoritics at the University of New Mexico and Brian Monteleone of WHOI, utilized meteorite samples provided by NASA from the asteroid 4-Vesta. The asteroid 4-Vesta, which formed in the same region of the solar system as Earth, has a surface of basaltic rock—frozen lava. These basaltic meteorites from 4-Vesta are known as eucrites and carry a unique signature of one of the oldest hydrogen reservoirs in the solar system. Their age—approximately 14 million years after the solar system formed—makes them ideal for determining the source of water in the inner solar system at a time when Earth was in its main building phase. The researchers analyzed five different samples at the Northeast National Ion Microprobe Facility—a state-of-the-art national facility housed at WHOI that utilizes secondary ion mass spectrometers. This is the first time hydrogen isotopes have been measured in eucrite meteorites.
The measurements show that 4-Vesta contains the same hydrogen isotopic composition as carbonaceous chondrites, which is also that of Earth. That, combined with nitrogen isotope data, points to carbonaceous chondrites as the most likely common source of water.
“The study shows that Earth’s water most likely accreted at the same time as the rock. The planet formed as a wet planet with water on the surface,” Marschall said.
While the findings don’t preclude a late addition of water on Earth, it shows that it wasn’t necessary since the right amount and composition of water was present at a very early stage.
“An implication of that is that life on our planet could have started to begin very early,” added Nielsen. “Knowing that water came early to the inner solar system also means that the other inner planets could have been wet early and evolved life before they became the harsh environments they are today.”
This research was supported by a Harriett Jenkins NASA graduate fellowship, an Andrew W. Mellon Foundation Award for Innovative Research, and a NASA Cosmochemistry award. The Northeast National Ion Microprobe Facility is supported by the National Science Foundation Instrumentation and Facilities Program.
Reference: “Early accretion of water in the inner solar system from a carbonaceous chondrite–like source” by Adam R. Sarafian, Sune G. Nielsen, Horst R. Marschall, Francis M. Mccubbin and Brian D. Monteleone, 31 October 2014, Science.
DOI: 10.1126/science.1256717






Be the first to comment on "Earth Received Most of Its Water Relatively Early from Chondrite-Like Bodies"