Google’s Quantum AI Challenges Long-Standing Physics Theories

Quantum simulators are now addressing complex physics problems, such as the dynamics of 1D quantum magnets and their potential similarities to classical phenomena like snow accumulation. Recent research confirms some aspects of this theory, but also highlights challenges in fully validating the KPZ universality class in quantum systems. Credit: Google LLC

Quantum simulators are revealing new insights into 1D quantum magnets, comparing their dynamics to phenomena like snow clumping.

Quantum simulators are advancing quickly and can now tackle issues previously confined to theoretical physics and numerical simulation. Researchers at Google Quantum AI and their collaborators demonstrated this new potential by exploring dynamics in one-dimensional quantum magnets, specifically focusing on chains of spin-1/2 particles.

They investigated a statistical mechanics problem that has been the focus of attention in recent years: Could such a 1D quantum magnet be described by the same equations as snow falling and clumping together? It seems strange that the two systems would be connected, but in 2019, researchers at the University of Ljubljana found striking numerical evidence that led them to conjecture that the spin dynamics in the spin-1⁄2 Heisenberg model are in the Kardar-Parisi-Zhang (KPZ) universality class, based on the scaling of the infinite-temperature spin-spin correlation function.

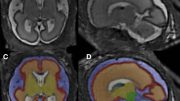
Simulating magnetization in a Heisenberg quantum spin chain. Credit: Google LLC

The KPZ equation was originally introduced to describe the stochastic, nonlinear dynamics of driven interfaces and has proven to apply to a wide range of classical systems, such as growing fronts of forest fires, that belong to the KPZ universality class. It would be surprising if the spin-1⁄2 Heisenberg model were in this universality class, as conjectured by the researchers at Ljubljana, because it is linear and non-stochastic, unlike the other systems in this class.

Experimental Insights from Quantum Simulations

In 2022, quantum simulations started shedding light on this question with cold atoms experiments carried out by researchers at the Max-Planck-Institut für Quantenoptik. By studying the relaxation of an initial imbalance of the magnetic spins, they found experimental evidence in support of this conjecture, which was published in Science in 2022.

To further explore spin dynamics in this model, the Google collaboration leveraged the ability of their superconducting quantum processor to quickly acquire large amounts of experimental data, allowing for a detailed study of the underlying statistics. Specifically, using a chain of 46 superconducting qubits, they measured the probability distribution of how many spins crossed the center of the chain, a quantity known as the transferred magnetization.

The mean and variance of this distribution showed behavior consistent with being in the KPZ universality class, in full agreement with the findings of the Max-Planck-Institut group. It was only when they carefully examined the third (skewness) and fourth (kurtosis) moments of the transferred magnetization that they found clear deviations from the predictions for the KPZ universality class, indicating that the conjecture does not hold on the timescales probed in the experiment.

Generally, measuring the distribution of a stochastic variable with sufficient precision such that the higher moments can be resolved with sufficient signal-to-noise is extremely challenging; it needs rapid sampling, a high level of control, and, for quantum processors, quantum coherence. This work, published in Science, excellently represents the current exciting era of quantum simulation, in which quantum processors allow for deepening our understanding of novel physical phenomena.

Reference: “Dynamics of magnetization at infinite temperature in a Heisenberg spin chain” by E. Rosenberg, T. I. Andersen, R. Samajdar, A. Petukhov, J. C. Hoke, D. Abanin, A. Bengtsson, I. K. Drozdov, C. Erickson, P. V. Klimov, X. Mi, A. Morvan, M. Neeley, C. Neill, R. Acharya, R. Allen, K. Anderson, M. Ansmann, F. Arute, K. Arya, A. Asfaw, J. Atalaya, J. C. Bardin, A. Bilmes, G. Bortoli, A. Bourassa, J. Bovaird, L. Brill, M. Broughton, B. B. Buckley, D. A. Buell, T. Burger, B. Burkett, N. Bushnell, J. Campero, H.-S. Chang, Z. Chen, B. Chiaro, D. Chik, J. Cogan, R. Collins, P. Conner, W. Courtney, A. L. Crook, B. Curtin, D. M. Debroy, A. Del Toro Barba, S. Demura, A. Di Paolo, A. Dunsworth, C. Earle, L. Faoro, E. Farhi, R. Fatemi, V. S. Ferreira, L. Flores Burgos, E. Forati, A. G. Fowler, B. Foxen, G. Garcia, É. Genois, W. Giang, C. Gidney, D. Gilboa, M. Giustina, R. Gosula, A. Grajales Dau, J. A. Gross, S. Habegger, M. C. Hamilton, M. Hansen, M. P. Harrigan, S. D. Harrington, P. Heu, G. Hill, M. R. Hoffmann, S. Hong, T. Huang, A. Huff, W. J. Huggins, L. B. Ioffe, S. V. Isakov, J. Iveland, E. Jeffrey, Z. Jiang, C. Jones, P. Juhas, D. Kafri, T. Khattar, M. Khezri, M. Kieferová, S. Kim, A. Kitaev, A. R. Klots, A. N. Korotkov, F. Kostritsa, J. M. Kreikebaum, D. Landhuis, P. Laptev, K.-M. Lau, L. Laws, J. Lee, K. W. Lee, Y. D. Lensky, B. J. Lester, A. T. Lill, W. Liu, A. Locharla, S. Mandrà, O. Martin, S. Martin, J. R. McClean, M. McEwen, S. Meeks, K. C. Miao, A. Mieszala, S. Montazeri, R. Movassagh, W. Mruczkiewicz, A. Nersisyan, M. Newman, J. H. Ng, A. Nguyen, M. Nguyen, M. Y. Niu, T. E. O’Brien, S. Omonije, A. Opremcak, R. Potter, L. P. Pryadko, C. Quintana, D. M. Rhodes, C. Rocque, N. C. Rubin, N. Saei, D. Sank, K. Sankaragomathi, K. J. Satzinger, H. F. Schurkus, C. Schuster, M. J. Shearn, A. Shorter, N. Shutty, V. Shvarts, V. Sivak, J. Skruzny, W. Clarke Smith, R. D. Somma, G. Sterling, D. Strain, M. Szalay, D. Thor, A. Torres, G. Vidal, B. Villalonga, C. Vollgraff Heidweiller, T. White, B. W. K. Woo, C. Xing, Z. Jamie Yao, P. Yeh, J. Yoo, G. Young, A. Zalcman, Y. Zhang, N. Zhu, N. Zobrist, H. Neven, R. Babbush, D. Bacon, S. Boixo, J. Hilton, E. Lucero, A. Megrant, J. Kelly, Y. Chen, V. Smelyanskiy, V. Khemani, S. Gopalakrishnan, T. Prosen and P. Roushan, 4 April 2024, Science.
DOI: 10.1126/science.adi7877