
Researchers have developed a quantum version of Archimedes’ screw that hauls fragile collections of gas atoms to higher and higher energy states without collapsing.
By adding some magnetic flair to an exotic quantum experiment, physicists produced an ultra-stable one-dimensional quantum gas with never-before-seen “scar” states – a feature that could someday be useful for securing quantum information.
As the story goes, the Greek mathematician and tinkerer Archimedes came across an invention while traveling through ancient Egypt that would later bear his name. It was a machine consisting of a screw housed inside a hollow tube that trapped and drew water upon rotation. Now, researchers led by Stanford University physicist Benjamin Lev have developed a quantum version of Archimedes’ screw that, instead of water, hauls fragile collections of gas atoms to higher and higher energy states without collapsing. Their discovery is detailed in a paper published today (January 14, 2021) in Science.
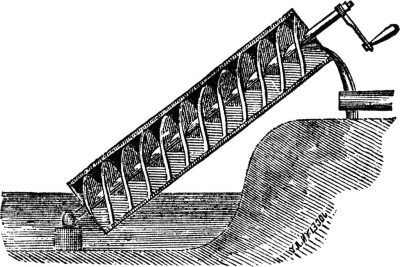
Experimental physicists have made a unique, one-dimensional quantum gas system that remains unusually stable as it’s pumped up to higher energy states. The researchers compare it to water being transported up an Archimedes’ screw.
“My expectation for our system was that the stability of the gas would only shift a little,” said Lev, who is an associate professor of applied physics and of physics in the School of Humanities and Sciences at Stanford. “I did not expect that I would see a dramatic, complete stabilization of it. That was beyond my wildest conception.”
Along the way, the researchers also observed the development of scar states – extremely rare trajectories of particles in an otherwise chaotic quantum system in which the particles repeatedly retrace their steps like tracks overlapping in the woods. Scar states are of particular interest because they may offer a protected refuge for information encoded in a quantum system. The existence of scar states within a quantum system with many interacting particles – known as a quantum many-body system – has only recently been confirmed. The Stanford experiment is the first example of the scar state in a many-body quantum gas and only the second ever real-world sighting of the phenomenon.
Super and stable
Lev specializes in experiments that extend our understanding of how different parts of a quantum many-body system settle into the same temperature or thermal equilibrium. This is an exciting area of investigation because resisting this so-called “thermalization” is key to creating stable quantum systems that could power new technologies, such as quantum computers.
In this experiment, the team explored what would happen if they tweaked a very unusual many-body experimental system, called a super Tonks-Girardeau gas. These are highly excited one-dimensional quantum gases – atoms in a gaseous state that are confined to a single line of movement – that have been tuned in such a way that their atoms develop extremely strong attractive forces to one another. What’s super about them is that, even under extreme forces, they theoretically should not collapse into a ball-like mass (like normal attractive gases will). However, in practice, they do collapse because of experimental imperfections. Lev, who has a penchant for the strongly magnetic element dysprosium, wondered what would happen if he and his students created a super Tonks–Girardeau gas with dysprosium atoms and altered their magnetic orientations ‘just so.’ Perhaps they would resist collapse just a little bit better than nonmagnetic gases?
“The magnetic interactions we were able to add were very weak compared to the attractive interactions already present in the gas. So, our expectations were that not much would change. We thought it would still collapse, just not quite so readily,” said Lev, who is also a member of Stanford Ginzton Lab and Q-FARM. “Wow, were we wrong.”
Their dysprosium variation ended up producing a super Tonks–Girardeau gas that remained stable no matter what. The researchers flipped the atomic gas between the attractive and repulsive conditions, elevating or “screwing” the system to higher and higher energy states, but the atoms still didn’t collapse.
Building from the foundation
While there are no immediate practical applications of their discovery, the Lev lab and their colleagues are developing the science necessary to power that quantum technology revolution that many predict is coming. For now, said Lev, the physics of quantum many-body systems out of equilibrium remain consistently surprising.
“There’s no textbook yet on the shelf that you can pull off to tell you how to build your own quantum factory,” he said. “If you compare quantum science to where we were when we discovered what we needed to know to build chemical plants, say, it’s like we’re doing the late 19th-century work right now.”
These researchers are only beginning to examine the many questions they have about their quantum Archimedes’ screw, including how to mathematically describe these scar states and if the system does thermalize – which it must eventually – how it goes about doing that. More immediately, they plan to measure the momentum of the atoms in the scar states to begin to develop a solid theory about why their system behaves the way it does.
The results of this experiment were so unanticipated that Lev says he can’t strongly predict what new knowledge will come from deeper inspection of the quantum Archimedes’ screw. But that, he points out, is perhaps experimentalism at its best.
“This is one of the few times in my life where I’ve actually worked on an experiment that was truly experimental and not a demonstration of existing theory. I didn’t know what the answer would be beforehand,” said Lev. “Then we found something that was truly new and unexpected and that makes me say, ‘Yay experimentalists!’”
Reference: “Topological pumping of a 1D dipolar gas into strongly correlated prethermal states” by Wil Kao, Kuan-Yu Li, Kuan-Yu Lin, Sarang Gopalakrishnan and Benjamin L. Lev, 14 January 2021, Science.
DOI: 10.1126/science.abb4928
Additional Stanford authors are graduate students Wil Kao (co-lead author), Kuan-Yu Li (co-lead author) and Kuan-Yu Lin. A professor from CUNY College of Staten Island and CUNY, New York, is also a co-author. Lev is also a member of Stanford Bio-X.
This research was funded by the National Science Foundation, Air Force Office of Scientific Research, Natural Sciences and Engineering Research Council of Canada and the Olympiad Scholarship from the Taiwan Ministry of Education.








Please add the journal link to the published paper.
Am I crazy for thinking they basically figured out how to stabilize entropy? Obviously we’re talking at a nano scale but in theory would it not eventually be the foundation for eternal life?
Yes.
The fundamentals of physics is evolving: decentralized expansion of the universe, change of speed of light in a vacuum, vanishing black holes, dark energy, cosmic energy, CERN extra dimension particles. Seems like we are a sequential multiverse. So freezing entropy locally may freeze it to become inconsistent with observable physics; decoherence.
I am guessing something different than eliminating entropy is happening.
Just a thought
That’s can be the new électric field for ALLS !
Why is space called space because as far as we know space could be a small and a way to run simulations with ways to be self sustaining
Most of the time, phenomena is too complicated to make predictions of outcome. It is best to do many experiments, and ask the material, what will you be or what will you do?
I wonder if quantum scar in conjunction with virtual remote magnetic core localization by the French physics team, could scale linear motion. A magnetic tractor beam.
A Space Elevator, Instead of a carbon nanotube cable, a moving stream of virtual magnetic cores.
Quantum scarring might provide the required resolution and malleable nature, to shape and manipulate the virtual core.
Of course a tractor beam has enormous other applications.
Motionless propulsion, black hole strength magnetic fields, stable planetary magnetic field for Venus, terreforming of Venus, decomposision of complex hazardous waste chemicals into simple recycled elements,moving coils of ionized gas, noninvasive surgery,water purification, stable magnetic structural members,floating real estate, wireless power transfer…
FINALLY, WE ARE PROCEEDING TO PROVE STRING THEORY