Revolutionizing Physics With a Game-Changing Topological Approach

A new experimental method developed by researchers enables the identification of topological properties in materials without relying on mathematical models, simplifying research and expanding the potential applications of topology in various fields. Credit: SciTechDaily.com

Innovative research introduces a practical, model-free method for exploring topological properties in materials, enhancing the scope and efficiency of topological studies.

The branch of mathematics known as topology has become a cornerstone of modern physics thanks to the remarkable – and above all reliable – properties it can impart to a material or system. Unfortunately, identifying topological systems, or even designing new ones, is generally a tedious process that requires exactly matching the physical system to a mathematical model.

Researchers at the University of Amsterdam and the École Normale Supérieure of Lyon have demonstrated a model-free method for identifying topology, enabling the discovery of new topological materials using a purely experimental approach.

Topology’s Evolution From Mathematics to Physics

Topology encompasses the properties of a system that cannot be changed by any ‘smooth deformation’. As you might be able to tell from this rather formal and abstract description, topology began its life as a branch of mathematics. However, over the last few decades physicists have demonstrated that the mathematics underlying topology can have very real consequences. Topological effects can be found in a wide range of physical systems, from individual electrons to large-scale ocean currents.

As a concrete example: in the field of quantum matter, topology rose to fame thanks to so-called topological insulators. These materials do not conduct electricity through their bulk, but electrons move freely along their surfaces or edges. This surface conduction will persist, unhindered by material imperfections, as long as you do not do something drastic like changing the entire atomic structure of the material. Moreover, currents on the surfaces or edges of a topological insulator have a set direction (depending on the electron spin), again enforced by the topological nature of the electronic structure.

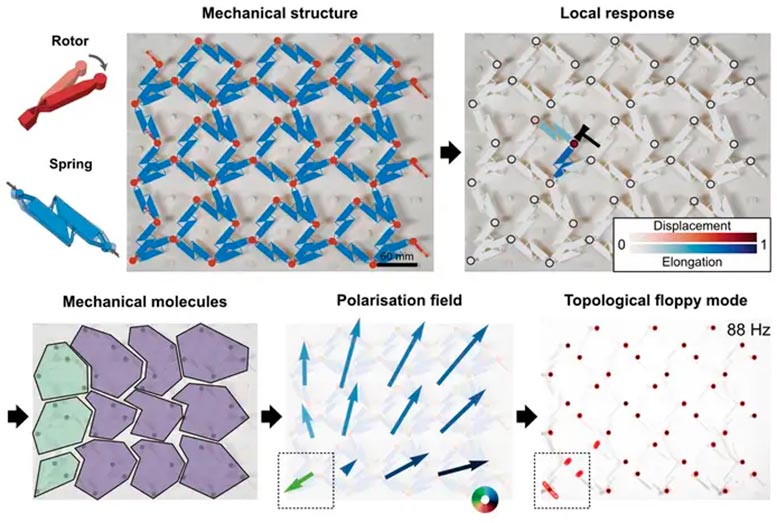
A fully experimental method for determining the topological character of a mechanical metamaterial. The metamaterial consists of a network of rotors (rigid rotating rods, red) connected by elastic springs (blue). By prodding an individual rotor and measuring the resulting movement in the metamaterial, it is possible to identify ‘mechanical molecules’ which behave like a single unit. By subsequently mapping out the ‘polarisation’ of each molecule, topological features of the metamaterial are easily identified. The bottom right image confirms the presence of a floppy corner mode – as predicted by the polarisation field – by shaking the entire metamaterial. Credit: University of Amsterdam.

Such topological features can have very useful applications, and topology has become one of the frontiers of materials science. Aside from identifying topological materials in nature, parallel research efforts focus on designing synthetic topological materials from the bottom up. Topological edge states of mechanical structures known as ‘metamaterials’ present unmatched opportunities for achieving reliable responses in wave guiding, sensing, computation, and filtering.

Impractical Mathematical Models

Research in this area is slowed down by the lack of experimental ways to investigate the topological nature of a system. The necessity of matching a mathematical model to a physical system limits research to materials for which we already have a theoretical description, and forms a bottleneck for identifying and designing topological materials. To tackle this issue, Xiaofei Guo and Corentin Coulais of the Machine Materials Laboratory at the University of Amsterdam teamed up with Marcelo Guzmán, David Carpentier, and Denis Bartolo of ENS Lyon.

“Until now, most experiments were intended to prove theories or showcase theoretical predictions in journals,” says Guo. “We found a way to measure topologically protected soft or fragile spots in unknown mechanical metamaterials without the need for modeling. Our approach allows for practical exploration and characterization of material properties without delving into complex theoretical frameworks.”

Practical Applications and Future Implications

The researchers demonstrated their method with mechanical metamaterials consisting of a network of rotors (rigid rods that can rotate) connected by elastic springs. Topology in these systems can make some regions of such a metamaterial, particularly floppy or stiff.

Bartolo explains, “We realized that selectively probing a material locally could give us all the necessary information to unveil soft or fragile spots in the structure, even in regions far removed from our probes. Using this, we developed a highly practical protocol applicable to a diverse range of materials and metamaterials.”

Prodding individual rotors in the metamaterial and tracking the resulting displacements and elongations in the system, the researchers identified different ‘mechanical molecules’: groups of rotors and springs that move as a single unit. In analogy to electrostatic systems, they then determined an effective ‘polarization’ of each molecule, calculated from the molecules’ movements. This polarization will suddenly flip direction in the presence of a topological feature, making inherent topology easy to identify.

The researchers applied their method to various mechanical metamaterials, some of which were known from previous studies to be topological, while others were new structures without an associated mathematical model. The results demonstrate that the experimentally determined polarisation is very effective in pointing out topological features.

This model-free approach is not just limited to mechanical systems; the same method could be applied to photonic or acoustic structures. It will make topology accessible to a broader range of physicists and engineers, and will make it easier to construct functional materials that go beyond laboratory demonstrations.

Reference: “Model-free characterization of topological edge and corner states in mechanical networks” by Marcelo Guzman, Xiaofei Guo, Corentin Coulais, David Carpentier and Denis Bartolo, 17 January 2024, Proceedings of the National Academy of Sciences.
DOI: 10.1073/pnas.2305287121