
The team of Rice University researchers was able to successfully use their versatile equations to predict the shapes of two different crystals: the truncated rectangle formed by 2D tin selenide (a promising thermo- and piezoelectric material) and the asymmetric needles formed by silver nitrite. These predictions were later confirmed through experimentation.
Rice theorists have developed a method that can accurately predict the shapes of crystals that do not have symmetry.
The shape of a crystal is determined by its inherent chemistry, which ultimately determines its final form from the most basic of details. However, the lack of symmetry in some crystals can make it difficult to predict their shape because the surface energies of their facets are unknown.
Researchers at Rice University believe that they have discovered a solution to the problem of predicting the shape of asymmetrical crystals by assigning arbitrary latent energies to their surfaces or, in the case of two-dimensional materials, edges.
Yes, it seems like cheating, but in the same way a magician finds a select card in a deck by narrowing the possibilities, a little algebraic sleight-of-hand goes a long way to solve the problem of predicting a crystal’s shape.
Rice University researchers have developed a method to predict how crystals take shape from their internal chemistry, even when the crystal lacks symmetry. This representation of a silver nitrate crystal has eight edges, none of which match the others. The Rice team’s algorithm was still able to predict its shape. Credit: Luqing Wang/Rice University
The method described in Nature Computational Science shows using what they call auxiliary edge energies can bring predictions back in line with the Wulff construction, a geometrical recipe in use for more than a century to determine how crystals arrive at their final equilibrium shapes.
The open-access paper by materials physicist Boris Yakobson, lead author and alumnus Luqing Wang and their colleagues at Rice’s George R. Brown School of Engineering introduces algorithms that employ arbitrary numbers for the right-hand factors in the equations and still deliver the proper unique shape-solution.
“The issue of shape is compelling, but researchers have been trying and failing for years to compute surface energies for asymmetrical crystals,” Yakobson said. “It turns out we were falling down a rabbit hole, but we knew that if nature can find a solution through a gazillion atomic movements, there should also be a way for us to determine it.”
He said the rise of interest in 2D materials in recent times motivated the new study. “We had a ‘eureka’ moment: After switching our geometrical thinking to algebraic we added closure equations that contain arbitrary parameters,” Yakobson said. “These seem useless, but we passed it all through the computer and observed a well-defined shape coming out,” he said.
“The hard part was convincing our reviewers that edge energy is truly undefinable, but a solution can still be achieved,” Wang said.
The work could provide a valuable tool to researchers who grow crystals from the bottom up for catalytic, light-emitting, sensing, magnetic and plasmonic applications, especially when their shapes and active edges are of particular importance.
The researchers pointed out that natural crystals enjoy the luxury of geological time. They arrive at their shapes by “relentlessly performing a trial-and-error experiment” as they seek equilibrium, the minimal energy of all their constituent atoms.
But computational and theoretical approaches simply can’t deal with billions of atoms at once, so they generally lean on the energies of outward-facing atoms. For many crystals that have equivalent facets or edges, that works just fine.
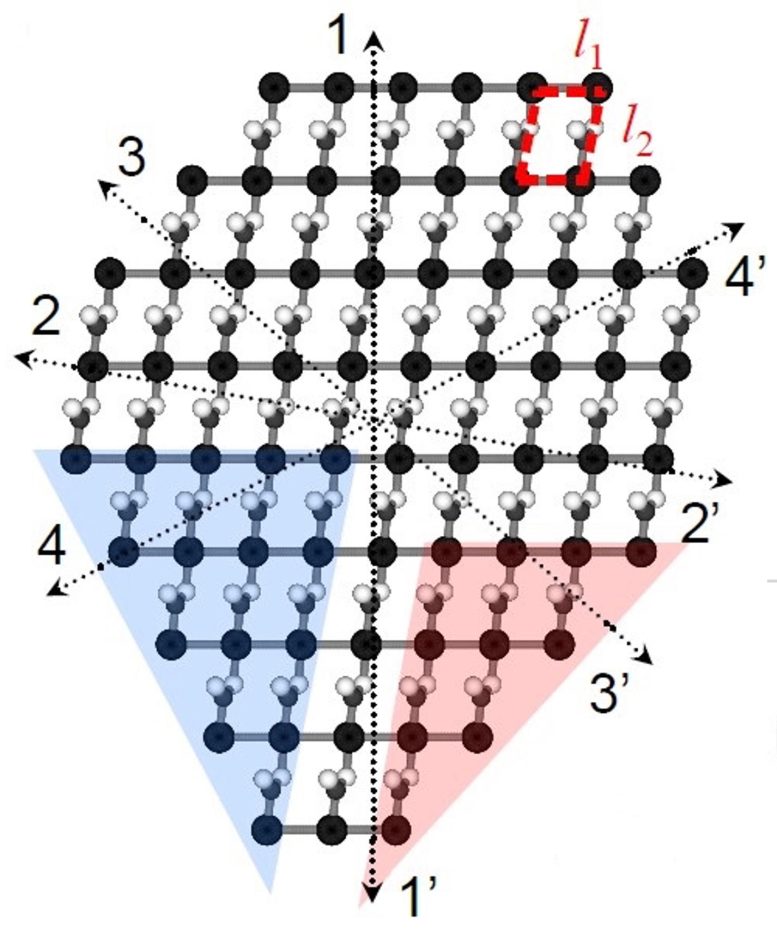
In 2D materials, essentially all of the atoms are “outward-facing.” When their edges are equivalent by symmetry — in rectangles, for instance — completing a Wulff construction is simple after calculating the edge energies via density functional theory.
But in the absence of symmetry, when all the edges are different, the calculated average energy is meaningless, Yakobson said.
“Nature has the answer to shape a crystal regardless of what it ‘knows’ or doesn’t about the edge energies,” he said. “So there is an answer. Our challenge was to mimic it with theory.”
The first step toward a solution was to consciously give up on finding the unknowable absolute edge energies and deal instead with their well-defined computable combinations, Yakobson said. Geometrically, this was quite a riddle, and for asymmetric bulk materials was hopelessly complicated.
“But 2D materials and their planar polygons made solving the problem easier to think about than having to deal with multifaceted polyhedra,” he said.
Finding and establishing average energies was just the first step, followed by “closure equations” that used arbitrary latent material energy for the right-hand side of the equation. Even if the latter numbers were intentionally incorrect, applying all to the textbook Wulff construction resulted in the correct crystal shape.
The group tested its theory on several 2D crystals and compared the results to the crystals’ observed final forms. Their versatile equations successfully predicted the shapes, shown experimentally, of the truncated rectangle formed by 2D tin selenide, a promising thermo-, and piezoelectric material, and the asymmetric needles formed by silver nitrite.
Reference: “Defining shapes of two-dimensional crystals with undefinable edge energies” by Luqing Wang, Sharmila N. Shirodkar, Zhuhua Zhang and Boris I. Yakobson, 28 November 2022, Nature Computational Science.
DOI: 10.1038/s43588-022-00347-5
The study was funded by the U.S. Department of Energy and the Army Research Office.








This article leaves a lot to be desired. It talks about 2D crystals, but the classic definition of a crystal is something with long-range three-dimensional regularity called a lattice. It also flips back and forth between talking about ‘crystals’ lacking symmetry and asymmetric ‘crystals.’ They are not the same. Perhaps they are talking about quasicrystals. However, that isn’t made clear. Whatever it is they are discussing, it doesn’t meet the classical definition of a crystal:
https://www.britannica.com/science/crystal/Ferrimagnetic-materials
Also, the article refers to silver nitrite, which albeit has very low symmetry (triclinic), is not truly lacking symmetry like in a glass or high-temperature liquid. The second figure mistakenly refers to silver nitrate instead of silver nitrite.