Scientists identify quantum geometry as crucial to process.
Researchers have produced new evidence of how graphene, when twisted to a precise angle, can become a superconductor, moving electricity with no loss of energy.
In a study published on February 15, 2023, in the journal Nature, the team led by physicists at The Ohio State University reported on their finding of the key role that quantum geometry plays in allowing this twisted graphene to become a superconductor.
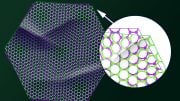
Graphene is a single layer of carbon atoms, the lead that is found in a pencil.
In 2018, scientists at the Massachusetts Institute of Technology discovered that, under the right conditions, graphene could become a superconductor if one piece of graphene were laid on top of another piece and the layers were twisted to a specific angle – 1.08 degrees – creating twisted bilayer graphene.
Ever since, scientists have been studying this twisted bilayer graphene and trying to figure out how this “magic angle” works, said Marc Bockrath, professor of physics at Ohio State and co-author of the Nature paper.
“The conventional theory of superconductivity doesn’t work in this situation,” Bockrath said. “We did a series of experiments to understand the origins of why this material is a superconductor.”
A Paradox in Electron Behavior
In a conventional metal, high-speed electrons are responsible for conductivity.
But twisted bilayer graphene has a type of electronic structure known as a “flat band” in which the electrons move very slowly – in fact at a speed that approaches zero if the angle is exactly at the magic one.
Under the conventional theory of superconductivity, electrons moving this slowly should not be able to conduct electricity, said study co-author Jeanie Lau, also a professor of physics at Ohio State.
With great precision, Haidong Tian, first author of the paper and a student in Lau’s research group, was able to obtain a device so close to the magic angle that the electrons were nearly stopped by usual condensed matter physics standards. The sample nevertheless showed superconductivity.
“It is a paradox: How can electrons which move so slowly conduct electricity at all, let alone superconduct? It is very remarkable,” Lau said.
In their experiments, the research team demonstrated the slow speeds of the electrons and gave more precise measurements of electron movement than had been previously available.
And they also found the first clues as to what makes this graphene material so special.
Quantum Geometry as the Key to Superconductivity
“We can’t use the speed of electrons to explain how the twisted bilayer graphene is working,” Bockrath said. “Instead, we had to use quantum geometry.”
As with everything quantum, quantum geometry is complex and not intuitive. But the results of this study have to do with the fact that an electron is not only a particle, but also a wave – and thus has wavefunctions.
“The geometry of the quantum wavefunctions in flat bands, together with the interaction between electrons, leads to the flow of electrical current without dissipation in bilayer graphene,” said co-author Mohit Randeria, professor of physics at Ohio State.
“We found that conventional equations could explain maybe 10% of the superconductivity signal we found. Our experimental measurements suggest quantum geometry is 90% of what makes this a superconductor,” Lau said.
The superconductive effects of this material can only be found in experiments at extremely low temperatures. The ultimate goal is to be able to understand the factors that lead to high-temperature superconductivity, which will be potentially useful in real-world applications, such as electrical transmission and communication, Bockrath said.
“It would have a huge impact on society,” he said. “It is a long way off, but this research is definitely taking us forward in understanding how it could happen.”
Reference: “Evidence for Dirac flat band superconductivity enabled by quantum geometry” by Haidong Tian, Xueshi Gao, Yuxin Zhang, Shi Che, Tianyi Xu, Patrick Cheung, Kenji Watanabe, Takashi Taniguchi, Mohit Randeria, Fan Zhang, Chun Ning Lau and Marc W. Bockrath, 15 February 2023, Nature.
DOI: 10.1038/s41586-022-05576-2
The Bockrath and Lau experimental groups, including graduate students Tian, Xueshi Gao, Yuxin Zhang, and Shi Che, collaborated with theorists Randeria at Ohio State, and Tianyi Xu, Patrick Cheung, and F. Zhang at the University of Texas at Dallas, and with scientists from the National Institute for Materials Science in Japan.
The study was supported by the Department of Energy Office of Science, the Ohio State Center for Emergent Materials, the National Science Foundation MRSEC, and the Army Research Office.
Never miss a breakthrough: Join the SciTechDaily newsletter.
Follow us on Google and Google News.
12 Comments
This is mind-boggling!
Because we have this one magic angle, there are probably other magic angles that do other magical things.
Time has nothing to do with geometry and heat energies . The magic angle is entirely inlegitimate. Please stop this educational government terrorism.
There is a Chinese saying to those who scoff and say, not possible. “Get out of way of man doing it.”
Maybe I’m completely off here, but it seems possible the current is carried by electron holes.
The artwork is full of 2D holes, I guess you could say. Generally, one does not think of electron holes outside of 3D semiconductors and hole conduction in a 1D wire doesn’t seem possible.
Broadly speaking hole conduction equates to allowing a lot of relatively side-to-side electron movement, which is nice because electrons inevitably want to oscillate anyway. A 2D sheet only allows 1 axis for side-to-side zig-zag type oscillation. seems to me that full access to hole current requires 2D side-to-side electron freedom, for helical oscillation.
With two graphene sheets, I tend to think of the result as a solid with a fractional extra dimension, putting it somewhere above 2D but below full 3D.
I mean current-wise side-to-side, where I refer to “side to side” carrier motion.
I don’t know that electron holes have to oscillate too, and it seems optimal if they don’t, because two electrons moving in opposite directions (leaving two holes) may avoid that. Maybe three graphene sheets (reversing the angle in a 1st try, I suppose) would offer some small temperature advantage.
I should add that a good model of gravity probably doesn’t hurt, but GR is unfortunately a perfectly bad model of gravity.
Can’t explain the angle yet. The Moire effect has a lattice size re-scaling that seems to carry light-like oscillation harmonics between the two graphene sheets. Maybe a prime number relation between Moire scale and atom lattice scale. Too large of a prime is maybe not needed and is too coarse for efficient jumps.
“Maybe three graphene sheets (reversing the angle …)”
Not a new idea, Forgot about this in other article, which shows four stacked sheets, giving three angle reversals.
MIT Physicists Discover a Family of “Magic” Superconducting Graphene Structures
“We can’t use the speed of electrons to explain how the twisted bilayer graphene is working …”
Zero macro-speed and non-zero micro-oscillation speeds can easily coexist, for what it’s worth. That may also be one reason electron mobility and electron hole mobility can also be different in the same material.